Fråga nr. 13 Provpass 1 (Kvant) Våren 2018
13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.
Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Är det möjligt att räkna ut det exakta avståndet mellan A och D utan att använda trigonometri?
Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Eftersom femhörningens omkrets är 75 cm så är varje sida 75/5 = 15 cm.
Avståndet mellan två närliggande hörn är 15 cm. Är avståndet mellan två andra hörn mindre än, lika med eller större än avståndet mellan två närliggande hörn?
Rita!
Hej
Svaret anser jag är rätt så trivialt. Om du behöver så rita upp en bild på femhörningen så ser du att kvantitet I är längden på en av femhörningens sidor. Avståndet från A till D är betydligt större en längden av en sida vilket du ser endast genom att kolla på bilden. Detta gör att B är korrekt.
Yngve skrev:Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Rita!
Jag har redan försökt rita! Men jag lyckades inte lösa uppgiften.
jonis10 skrev:Hej
Svaret anser jag är rätt så trivialt. Om du behöver så rita upp en bild på femhörningen så ser du att kvantitet I är längden på en av femhörningens sidor. Avståndet från A till D är betydligt större en längden av en sida vilket du ser endast genom att kolla på bilden. Detta gör att B är korrekt.
Jag förstår vad du menar. Fast jag vill veta hur de tänk att man skall beräkna denna längd med matte 1 eller 2 kunskaper.
Aion skrev:Yngve skrev:Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Rita!
Jag har redan försökt rita! Men jag lyckades inte lösa uppgiften.
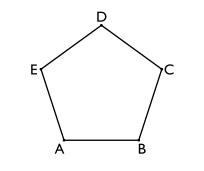
Blir det tydligare nu?
Aion skrev:
Jag förstår vad du menar. Fast jag vill veta hur de tänk att man skall beräkna denna längd med matte 1 eller 2 kunskaper.
Ingen har begärt att du skall beräkna längden.
jonis10 skrev:Aion skrev:Yngve skrev:Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Rita!
Jag har redan försökt rita! Men jag lyckades inte lösa uppgiften.
Blir det tydligare nu?
Jag förstår inte vad du menar? AD ser ut att vara större. Men det där är ju inte en lösning. Bara en bra gissning.
Aion skrev:jonis10 skrev:Aion skrev:Yngve skrev:Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Rita!
Jag har redan försökt rita! Men jag lyckades inte lösa uppgiften.
Blir det tydligare nu?
Jag förstår inte vad du menar? AD ser ut att vara större. Men det där är ju inte en lösning. Bara en bra gissning.
Ja. AD är kvantitet II.
Det betyder att kvantitet II är större än kvantitet I, dvs svar B är korrekt.
Du behöver inte göra fullständiga lösningar på denna delen av HP och du kommer inte heller att hinna göra det.
Smutstvätt skrev:*Reklam*
Tips för framtiden: Kolla in denna tråd.
*Slut på reklam*
Jag har sett vad du skrev. Men du gav inte någon lösning i denna tråd.
Yngve skrev:Aion skrev:jonis10 skrev:Aion skrev:Yngve skrev:Aion skrev:13. Omkretsen av den regelbundna femhörningen ABCDE är 75 cm.
Kvantitet I: 15 cm
Kvantitet II: Avståndet från punkten A till punkten D
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig.Om jag räknat rätt får man via trigonometri att AD = 30(sin(54°)) ≈ 24.27 men jag kan inte beräkna sin(54) utan en miniräknare lol.
Jag ser att man tycks behöva hänvisa till triangelolikheten : https://sv.wikipedia.org/wiki/Triangelolikheten. Men är verkligen linjär algebra ett kunskapskrav för högskoleprovet?!
Rita!
Jag har redan försökt rita! Men jag lyckades inte lösa uppgiften.
Blir det tydligare nu?
Jag förstår inte vad du menar? AD ser ut att vara större. Men det där är ju inte en lösning. Bara en bra gissning.
Ja. AD är kvantitet II.
Det betyder att kvantitet II är större än kvantitet I, dvs svar B är korrekt.
Du behöver inte göra fullständiga lösningar på denna delen av HP och du kommer inte heller att hinna göra det.
Så de vill alltså att man skall gissa? De som skapade detta prov måste vara dumma i huvudet xD. Det är ju ett helt meningslös prov om man resonerar på detta sättet.
Nej, du ska inte gissa. Du ska undersöka figuren och dra den rimliga slutsatsen att sträckan AD är längre än sträckan AE.
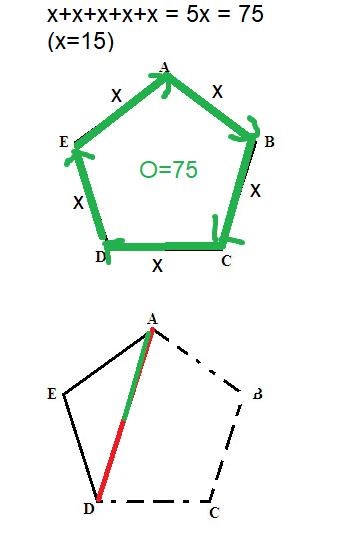
Kolla där. En sida är 15cm. Den gröna i nedre figuren representerar en sådan sida. Ser du att en sida är i princip hälften av sträckan.
sprite111 skrev:
Kolla där. En sida är 15cm. Den gröna i nedre figuren representerar en sådan sida. Ser du att en sida är i princip hälften av sträckan.
Haha snygg ritning! Men det är ändå inte ett formellt bevis. Jag hittade dock ett vilket jag hänvisar till nedan:
Euclid Vol.1 Proposition 20.
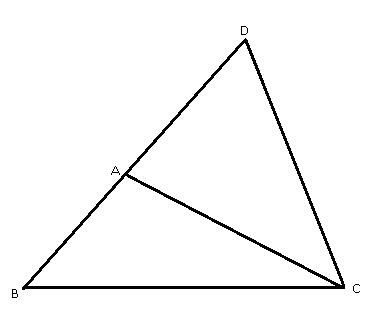
In any triangle, two sides taken together in any manner are greater than the remaining one.
For let ABC be a triangle;
I say that in the triangle ABC two sides taken together in any manner are greater than the remaining one, namely
BA, AC greater than BC,
AB, BC greater than AC,
BC, CA greater than AB.
For let BA be drawn through to the point D,
let DA be made equal to CA, and let DC be joined.
Then, since DA is equal to AC,
the angle ADC is also equal to the angle ACD; [1.5]
therefore the angle BCD is greater than the
angle ADC. [C. N. 5]
And, since DCB is a triangle having the angle BCD
greater than the angle BDC,
and the greater angle is subtended by the greater side,
[1. 19]
therefore DB is greater than BC.
But DA is equal to AC;
therefore BA, AC are greater than BC.
Similarly, we can prove that AB, BC are also greater
than CA, and BC, CA than AB.
Therefore etc.
Q.E.D
It was the habit of the Epicureans, says Proclus (p. 322), to ridicule this theorem as being evident even to an ass and requiring no proof, and their allegation that the theorem was "known" even to an ass was based on the fact that, if fodder is placed at one angular point and the ass at another, he does not, in order to get to his food, traverse the two sides of the triangle but only the one side separating them ( an argument which makes Savile exclaim that its authors were "digni ipsi, qui cum Asino foenum essent," p.78). Proclus replies truly that a mere perception of the truth of the theorem is a different thing from a scientific proof of it and a knowledge of the reason why it is true. Moreover, as Simson says, the number of axioms should not be increased without necessity.
Hahaha ;) tack lärt mig från de bästa *host* smutstvätt *host* :=]
--
ABCDABCDVDCAVDBDACBDAB så ser jag den där texten. =)
Hehe bra att du delar med dig så kan andra intresserade se!
Men har du fått rätsida på uppgiften nu?





