Fråga om karakteristiska polynomet och diagonalisering

Hej,

Jag hoppas ni har en bra dag. Jag sitter fast med en uppgift som handlar om diagonalisering och egenvärden, och jag skulle verkligen uppskatta lite hjälp för att klara den. Jag har försökt förstå koncepten, men jag känner att jag har kört fast.

Här är den specifika uppgiften jag försöker lösa:

Uppgift:

Vi har en matris $A$ som kan faktoriseras som $A = PDP^{-1}$ , där:
$A = \begin{bmatrix}1 & 0 & -2 \-1 & 2 & -2 \ & -3 & 1\end{bmatrix}$
och
$D = \begin{bmatrix}2 & 0 & 0 \0 & -1 & 0 \0 & 0 & 3\end{bmatrix}$

(a) Jag behöver visa att det karakteristiska polynomet för $A$ kan skrivas som $(\lambda - 2)(\lambda + 1)(\lambda - 3)$ .

(b) Jag behöver även beräkna matrisen $P$ .

Jag skulle verkligen uppskatta om någon kunde ge mig en steg-för-steg förklaring för att lösa dessa problem. Alla insikter, tips eller hänvisningar till resurser som kan hjälpa mig förstå koncepten och tillämpa dem korrekt skulle vara otroligt värdefulla för mig.

Jag har försökt förstå detta med egenvärden och diagonalisering, men jag kämpar med de finare detaljerna. Tack på förhand för er hjälp.

Någonting här kanske går att använda: https://sv.wikipedia.org/wiki/Egenv%C3%A4rde,_egenvektor_och_egenrum

Det karaktäristiska polynomet för A kan definieras som

p( $λ$ ) = det( $λ$ I - A).

Du kan tex börja med att visa att D har samma karaktäristiska polynom som A. Sedan är det lätt att ta fram polynomet.

PATENTERAMERA skrev:
Det karaktäristiska polynomet för A kan definieras som

p( $λ$ ) = det( $λ$ I - A).

$D=\begin{bmatrix}2&0&0\\ 0&-1&0\\ 0&0&3\end{bmatrix}$

$p\left( \lambda \right) =det\left( A-\lambda I\right) =\begin{vmatrix}1-\lambda &0&-2\\ -1&2-\lambda &-2\\ 1&-3&1-\lambda \end{vmatrix}$

För att beräkna determinanten av denna 3x3-matris får vi fram att:

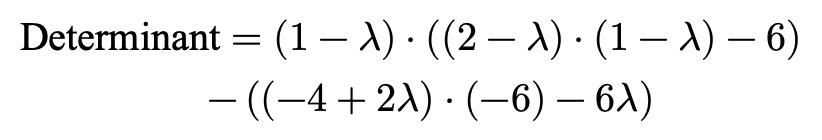
Vilket förenklas till $\lambda^{3} -3\lambda^{2} -22\lambda +24$

Är det rätt så långt?

Du kan tex börja med att visa att D har samma karaktäristiska polynom som A. Sedan är det lätt att ta fram polynomet.

Jag såg en video som förklarade att en matris med endast diagonalelement har de egenvärdena som finns i tr(A), dvs $\lambda = tr(A)$ . Hur härleder man detta, vet inte om denna motivation är tillräckligt god för min lärare. Vad säger detta om karakteristiska polynomet?

Nja, du tänker nog på att tr(A) = summan av egenvärdena.

Och det(A) = produkt av egenvärden.

Du kan kolla själv. Stämmer det med svaret i a)? Är ditt polynom lika med

$(λ - 2) (λ - 3) (λ + 1)$ ? Om inte, får du räkna om.

PATENTERAMERA skrev:
Nja, du tänker nog på att tr(A) = summan av egenvärdena.

Och det(A) = produkt av egenvärden.

Du kan kolla själv. Stämmer det med svaret i a)? Är ditt polynom lika med

$(λ - 2) (λ - 3) (λ + 1)$ ? Om inte, får du räkna om.

Jag märker att den determinant jag beräknade inte var korrekt. Jag började om genom att använda kofaktorutveckling:

= (1-λ) * det([2-λ, -2; -3, 1-λ]) - 0 * det([-1, -2; 1, 1-λ]) + (-2) * det([-1, 2-λ; 1, -3])

Beräknade minorna:

= (1-λ) * (λ^2 - 3λ - 4) - 0 * (λ + 1) + (-2) * (λ + 1)

Förenklade sedan:

(1-λ) * (λ^2 - 3λ - 4) - 0 * (λ + 1) + (-2) * (λ + 1) = -λ^3 + 4λ^2 - λ - 6

Resultatet blir:

= -λ^3 + 4λ^2 - λ - 6

Och det verkar inte bli samma svar som det man vill ha i (a):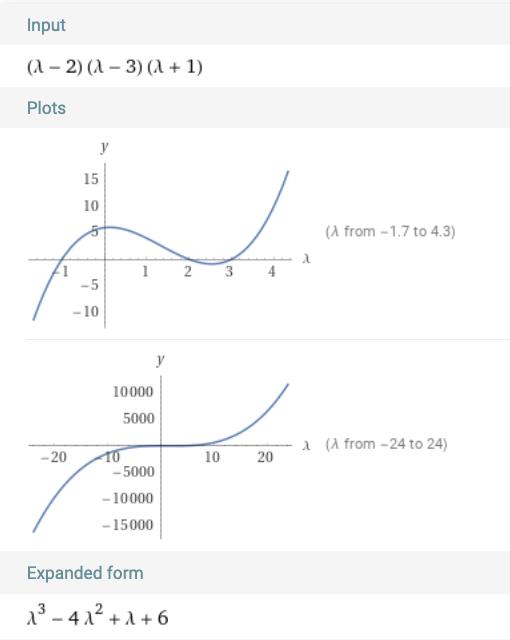

Det är i princip samma. Man kan definiera polynomet på olika sätt.

p(lambda) = det(lambda x I - A) eller p(lambda) = det(A - lambda x I).

De verkar ha tagit den första definitionen och du den andra definitionen. Det blir dock endast en teckenskillnad.

Om du multiplicerar deras polynom med -1 så får du ditt polynom. Men nollställena (egenvärdena) blir de samma.

Vi kan visa att D och A har samma k-polynom.

det(lambda x I - A) = det(lambda x I - PDP^-1) = det(P(lambda x I - D)P^-1) = det(P^-1P(lambda x I - D)) = det(lambda x I - D).

Att det karakteristiska polynomet till D blir (lambda - 2)(lambda + 1)(lambda - 3) är trivialt att visa.

Svara

Visa senaste svar