9 svar

136 visningar

dajamanté behöver inte mer hjälp

Fräscha zombier: integraler, algebra, andra derivata, allt möjligt blev fel

En till uppgift där jag märkte att jag egentligen hade inga koll på kedjeregeln och andra derivata:

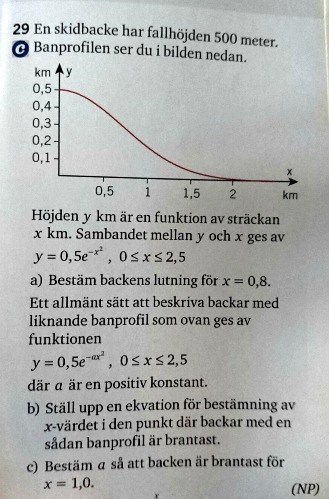
a) Så först hade jag jättesvårt att derivera funktionen, för jag blev förvirrad mellan sammansätta funktion och vanliga e funktioner.

Visst en sammansätt funktion $f (g x)$ deriveras $f' (g x) + g' (x)$ ?

Om jag deriverar $0, 5 e^{- x^{2}}$ varför får jag inte $0, 5 e^{- u} \to (- 1) * 0, 5 e^{- u} * u' \to (- 1) * 0, 5 e^{- x^{2}} * - 2 x \to 0, 5 x e^{- x^{2}}$

Hur känner jag igen en sammansätt funktion? Till exempel är $e^{\frac{- x}{a}}$ en sammansätt funktion eller en vanligt $e^{k x}$ som man deriverar med att sätta faktorn k framme?

b) och c) Där har jag helt glömt att det var andraderivata man var efter, jag tänkte att den är brantast där e^ax=1 (lite grand som sin/cos)... Men iaf efter många tårar och svett och den gamla pluggakuten kom jag fram till:

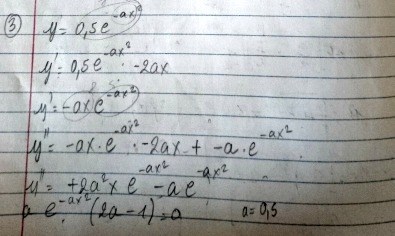
Vad spelar det för roll att x=1 för att hitta den brantaste punkt? Uttrycket $e^{- a x^{2}} (2 a - 1) = 0$ kommer väl alltid att bli noll för a=0,5?

Daja skrev :
Om jag deriverar $0, 5 e^{- x^{2}}$ varför får jag inte $0, 5 e^{- u} \to (- 1) * 0, 5 e^{- u} * u' \to (- 1) * 0, 5 e^{- x^{2}} * - 2 x \to 0, 5 x e^{- x^{2}}$

Om du deriverar 0,5e^(-x^2) så får du 0,5e^(-x^2) multiplicerat med inre derivatan, som är derivatan av -x^2, dvs -2x.

Det hela blir 0,5e^(-x^2) * (-2x) = -x*e^(-x^2).

Hur känner jag igen en sammansätt funktion? Till exempel är $e^{\frac{- x}{a}}$ en sammansätt funktion eller en vanligt $e^{k x}$ som man deriverar med att sätta faktorn k framme?

Båda är sammansatta funktioner.

Den ena har inre derivatan -1/a och den andra har inre derivatan k.

Det är bara det att vi har lärt oss deriveringsregeln för e^(kx) utantill. Men det är ändå kedjeregeln som ligger bakom.

Daja skrev :

Du har missat lite vid förenklingen av andraderivatan.

Det ska vara

y'' = 2a^2x^2*e^(-ax^2) - a*e^(-ax^2).

y'' = ae^(-ax^2)*(2ax^2 -1).

Nähä.. båda var sammansätta funktioner...

Ok nu får se... :

$y = 0, 5 e^{- a x^{2}} y' = 0, 5 e^{- a x^{2}} * - 2 a x = - a x * e^{- a x^{2}} y'' = - a x * e^{- a x^{2}} * - 2 x + - a * e^{- a x^{2}} = - 2 a^{2} x^{2} * e^{- a x^{2}} - a e^{- a x^{2}} = a e^{- a x^{2}} (2 a x - 1)$

Ok, isf x:an blir relevant!

Daja skrev :
Nähä.. båda var sammansätta funktioner...
Ok nu får se... :
$y = 0, 5 e^{- a x^{2}} y' = 0, 5 e^{- a x^{2}} * - 2 a x = - a x * e^{- a x^{2}} y'' = - a x * e^{- a x^{2}} * - 2 x + - a * e^{- a x^{2}} = - 2 a^{2} x^{2} * e^{- a x^{2}} - a e^{- a x^{2}} = a e^{- a x^{2}} (2 a x - 1)$
Ok, isf x:an blir relevant!

Du slarvar, tappar en faktor a i andraderivatans första term (men den dyker upp i nästa steg), och en faktor x innanför parentesen i sista uttrycket.

Pff ok jag tror jag måste gå och träna, choklad hjälper absolut inte.

Jag går på en gång.

*ropar ut genom dörren till den till träning flyende Daja*

"Hallå vänta! Jag glömde säga att du även fick fel tecken på första termen i näst sista steget!"

;-)

Haha lol!

Ok, hoppas att jag har bättre fungerande hjärna nu.... vilket press! När jag är osaker slarvar jag ännu mer...

$y = 0, 5 e^{- a x 2}$

Så om vi ta det lungt, den första term förändras inte och stannar sig själv. Den multipliceras med sitt inre derivata...

$y = 0, 5 e^{- a x^{2}} * - 2 a x = - a x e^{- a x^{2}}$ . Det måste vara rätt yxan eftersom du sa inget om det ;)

Nu ta vi den ännu lugnare och deriverar försiktigt i rosa...

$y' = - a x * e^{- a x^{2}}$

$y'' = - a * e^{- a x^{2}} + - a x * e^{- a x^{2}} * - 2 a x$ som borde ge oss $+ 2 a^{2} x^{2} e^{- a x^{_{2}}} - a e^{- a x^{2}}$ (där har jag en plus och en minus tecken i mottsats till 2 post tidigare :)...

Om jag drar försiktigt ut en faktor $a e^{- a x^{2}}$ ur den här härligt blandning som är lika ostabilt och rörig som en tonårskärleksaffär.....

Får jag $a e^{- a x^{2}} (2 a x - 1)$ ??

Haha.

Ja nästan.

Kolla sista steget igen, där du nästan tillräckligt f-ö-r-s-i-k-t-i-g-t drog ut faktorn.

Vad ska det egentligen bli kvar?

...

Tips: Håll ögonen på det där busiga x-et som bara springer och gömmer sig hela tiden.

Ah gud det är sant! Jag har tappat en x i första termet!! Jag lovar att jag försöker att inte slarva, men det liksom går inte :'(

Svara

Visa senaste svar