Friktionskraft för bil i cirkulärbana (Fysik/Universitet)

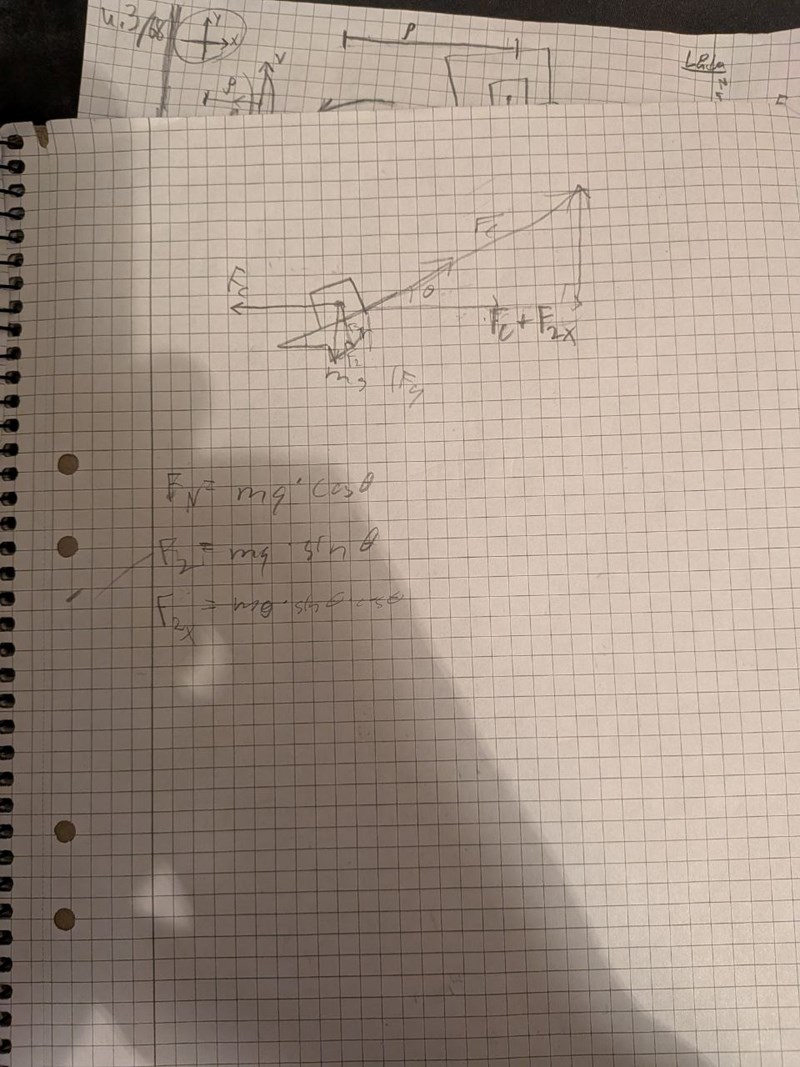
Asså antingen är det så att de vill ha storleken skrivet med friktionskraftens y och x komponenter och roten ur det eller så ska man ta med normalkraften och sen skriva en kraftsumma ekvation.

Edit: nej vänta, frågan är om det verkligen = 0 (för kraftjämvikt) för den accelererar ju fortfarande inåt?

Edit 2: Jag kan ha fel om vad F_c egentligen är, hmm...

Edit 3: Har jag fel om friktionkraftens riktning också??

Edit 4: Centripetalkraft är egentligen inte en kraft, justee, det är en samling av andra krafter!!!

Ja, för att bilen och lådan ska röra sig i en cirkelbana med konstant fart (dvs accelerera) måste resultanten av krafterna motsvara "centripetalkraften". I det här fallet måste lådan accelereras in mot cirkelrörelsens centrum.

Men om man vill kan man fuska lite och införa något som kallas fiktiva krafter, det kan ibland kännas enklare att räkna på. Regeln är då att fuskkraften ska angripa i masscentrum och införas med motsatt tecken (mot referensramens acceleration).

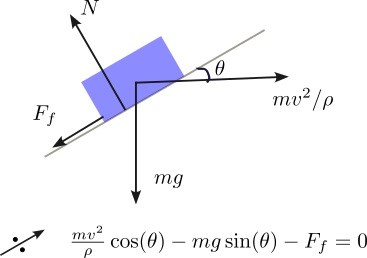
Här låtsas vi alltså att lådan ligger stilla och den fiktiva kraften $mv^2/\rho$ pekar då bort från accelerationscentrum, det är den "kraften" som gör att det känns som att lådan ska flyga av lastbilen. Eller den kraft som trycker oss utåt i en karusell. Fiktiva krafter används för accelererade referensramar och beskriver hur det känns för någon som står "stilla" i det roterande systemet. Testa att räkna på båda sätten och se vilket som känns lättast. Det viktiga är att du inte blir förvirrad av tecken och riktning!

D4NIEL skrev:
Det viktiga är att du inte blir förvirrad av tecken och riktning!

Jag tror jag nyss blev det! Jag tror jag ska starta en ny tråd vad det gäller tecken och riktning för får fel på det ofta. I bilden nedan kom jag fram till vad friktionskraften är men tecken på normalkraften kan vara fel samt för friktionskraften (dessutom hade jag inte med rho eller hastigheten så det sket sig)lol! Okej man ska försöka med din metod men redan nu när jag ser på den har jag två frågor!

1. Varför är friktionskraften riktad neråt? Jag är van vid att (kanske bara gäller vid stillastående idk) att friktionskraften är riktad snett uppåt.

2. Varför är inte centripetalkraften riktad mot centrum, d.v.s. mot vänster om den ändå utgörs av andra krafter?

3. Jag fattar heller inte din ekvation du kom fram till och varför du valt att lägga ihop dem på det sättet. Varför tar du cos( $θ$ ) multiplicerat med F_C, jag trodde redan den var den närliggande kraften?

Edit: din givna ekvation gav rätt svar dock skulle man byta tecken. Again, förstår inte riktigt lol.

Edit 2: tror det ska stå "+F" för att ge det rätta svaret

1. Friktionskraftens riktning beror på hur fort lastbilen kör och hur mycket kurvan lutar, men i de flesta fall är kurvans lutning liten och hastigheten 70-100km/h samtidigt som kurvradien är åtminstone 100-200m. Om vi byter riktning på $F_f$ får vi

$F_f=mg\sin(\theta)-mv^2/\rho\cos(\theta)$

Och den kraften är givet hastighet $v$ , $g$ och $\rho$ oftast mindre än noll. Om man kör för fort med lastbilen i en kurva orkar inte friktionskraften hålla kvar lådan på flaket och lådan börjar glida åt höger. Så för mig är det mer naturligt att låta $F_f$ peka åt andra hållet. Men det spelar ju ingen roll, det enda som händer är att man får en negativ kraft när man sätter in värden. Och då vet man att den egentligen pekar åt andra hållet :-)

2. 3. Du kan räkna utan fiktiva krafter på det dynamiska fallet, då ser det ut så här:

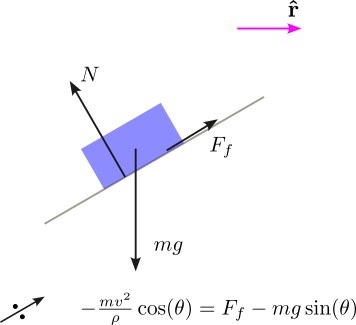
Här har jag vänt på $F_f$ och satt upp $F=ma$ utmed planet. Orsaken till att vi måste multiplicera med $\cos(\theta)$ är att accelerationen är riktad som den rosa pilen på bild. Och jag räknar ju utmed planet. Om du istället räknar i $\hat{r}$ -led så får du räkna ut komposanten av $F_f$ och $N$ (krångligare, tycker jag!). Är du med?

I min första lösning använde jag en fiktiv kraft och lät summan av alla krafter vara noll.

I min andra lösning använde jag att F=ma, summan av krafterna ska vara lika med massan gånger accelerationen.

Båda metoderna ger såklart samma svar.

D4NIEL skrev:
1. Friktionskraftens riktning beror på hur fort lastbilen kör och hur mycket kurvan lutar, men i de flesta fall är kurvans lutning liten och hastigheten 70-100km/h samtidigt som kurvradien är åtminstone 100-200m. Om vi byter riktning på $F_f$ får vi

$F_f=mg\sin(\theta)-mv^2/\rho\cos(\theta)$

Och den kraften är givet hastighet $v$ , $g$ och $\rho$ oftast mindre än noll. Om man kör för fort med lastbilen i en kurva orkar inte friktionskraften hålla kvar lådan på flaket och lådan börjar glida åt höger. Så för mig är det mer naturligt att låta $F_f$ peka åt andra hållet. Men det spelar ju ingen roll, det enda som händer är att man får en negativ kraft när man sätter in värden. Och då vet man att den egentligen pekar åt andra hållet :-)

2. 3. Du kan räkna utan fiktiva krafter på det dynamiska fallet, då ser det ut så här:

Här har jag vänt på $F_f$ och satt upp $F=ma$ utmed planet. Orsaken till att vi måste multiplicera med $\cos(\theta)$ är att accelerationen är riktad som den rosa pilen på bild. Och jag räknar ju utmed planet. Om du istället räknar i $\hat{r}$ -led så får du räkna ut komposanten av $F_f$ och $N$ (krångligare, tycker jag!). Är du med?

I min första lösning använde jag en fiktiv kraft och lät summan av alla krafter vara noll.

I min andra lösning använde jag att F=ma, summan av krafterna ska vara lika med massan gånger accelerationen.

Båda metoderna ger såklart samma svar.

Vänta när ska man använda sig av fiktiva krafter tycker du? Det är helt nytt för mig.

Man ska använda fiktiva krafter när det blir enklare räkningar. Men om ni inte gått igenom det ännu är det pedagogiskt dumt av mig att förvirra dig. Vänta med det tills ni gått igenom vad det är.

Sätt alltså upp Newtons andra lag utmed "planet", då behöver du bara komposantuppdela accelerationen och mg. En annan fördel med att räkna utmed planet är att du inte behöver blanda in $N$ , som ju är vinkelrät mot planet.

D4NIEL skrev:
Man ska använda fiktiva krafter när det blir enklare räkningar. Men om ni inte gått igenom det ännu är det pedagogiskt dumt av mig att förvirra dig. Vänta med det tills ni gått igenom vad det är.

Sätt alltså upp Newtons andra lag utmed "planet", då behöver du bara komposantuppdela accelerationen och mg. En annan fördel med att räkna utmed planet är att du inte behöver blanda in $N$ , som ju är vinkelrät mot planet.

Ska inte ljuga, jag fattar fortfarande inte varför vi tar gånger cos ( $θ$ ) om ändå centripetalkraften är i samma riktning som r. Tror jag är för trött för det här ngl.

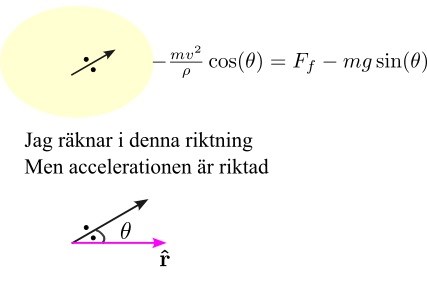
Eller ja, mer exakt är accelerationen $\mathbf{a}=(-r\dot{\theta}^2)\mathbf{\hat{r}}=-v^2/\rho \mathbf{\hat{r}}$ , men jag hoppas du förstår vad jag menar :-)

Det står alltså $ma=F_{tot}$ i riktning snett uppåt planet. Så vi har komposantuppdelat accelerationen.

D4NIEL skrev:

Eller ja, mer exakt är accelerationen $\mathbf{a}=(-r\dot{\theta}^2)\mathbf{\hat{r}}=-v^2/\rho \mathbf{\hat{r}}$ , men jag hoppas du förstår vad jag menar :-)

Det står alltså $ma=F_{tot}$ i riktning snett uppåt planet. Så vi har komposantuppdelat accelerationen.

Okej snabb fråga bara, varför har du två prickar runt pilen?

Det är en riktningsmarkering för projektion av ekvationen. Om man bara ritar en pil kommer många tro att det är en vektor av något slag. Så man sätter dit prickarna som ett didaktiskt hjälpmedel.

Det är ganska vanligt att man använder beteckningen i mekanik och hållfasthetslära. Ursprungligen tror jag symbolen kommer från rittekniken där den betyder “tagen i denna riktning”.

Tanken här är alltså att vi ska projicera hela systemet utmed planet, riktning uppåt planet. Det innebär att allt som pekar uppåt planet går in med positivt tecken, och allt som pekar nedåt planet får ett minustecken.

Vektorer som inte är parallella med planet måste projiceras. Vektorer som är vinkelräta mot planet (till exempel $N$ ) kan vi helt strunta i.

D4NIEL skrev:
Det är en riktningsmarkering för projektion av ekvationen. Om man bara ritar en pil kommer många tro att det är en vektor av något slag. Så man sätter dit prickarna som ett didaktiskt hjälpmedel.

Det är ganska vanligt att man använder beteckningen i mekanik och hållfasthetslära. Ursprungligen tror jag symbolen kommer från rittekniken där den betyder “tagen i denna riktning”.

Tanken här är alltså att vi ska projicera hela systemet utmed planet, riktning uppåt planet. Det innebär att allt som pekar uppåt planet går in med positivt tecken, och allt som pekar nedåt planet får ett minustecken.

Vektorer som inte är parallella med planet måste projiceras. Vektorer som är vinkelräta mot planet (till exempel $N$ ) kan vi helt strunta i.

Ahh jag tror jag förstår det nu så kolla positiv riktning har vi nu omdefinierat som snett uppåt höger och friktionskraften går uppåt i den riktningen alltså blir den bara positiv.

Vi projicerar nu både F_c och den tangential kraften från tyngdkraften. Då får vi -mg sin( $θ$ ) vilket är PRECIS i motsatt riktning till friktionskraften F_foch därför subtraheras de i högerledet. Sen eftersom centripetalkraften är i motsatt riktning och vi definierat r positivt till höger så blir den negativ men sen så följer den inte riktningen direkt så då måste vi projicera F_c på riktningsmarkeringen. Har jag förstått dig rätt?

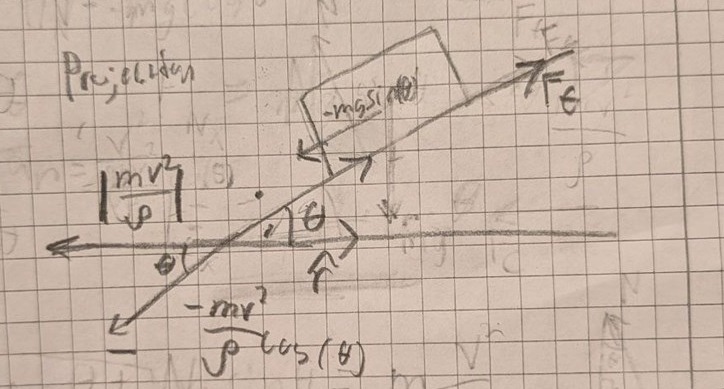
Ja, det låter korrekt!

Det du kallar centripetalkraften är alltså $\mathbf{F}_c=m\mathbf{a}$ projicerad utmed planet.

Och det du gör är att ställa upp projektionen av ekvationen $\mathbf{F}_{tot}=m\mathbf{a}$ utmed planet i riktning uppåt planet.

Centripetalkraften är den kraft som behövs för att hålla kvar lådan i en cirkelbana (accelerera lådan exakt lagom mycket), och den kraften ska ju vara summan av krafterna som verkar på lådan.

D4NIEL skrev:
Ja, det låter korrekt!

Det du kallar centripetalkraften är alltså $\mathbf{F}_c=m\mathbf{a}$ projicerat utmed planet.

Och det du gör är att ställa upp projektionen av ekvationen $\mathbf{F}=m\mathbf{a}$ utmed planet i riktning uppåt planet.

Aa precis. Nu har jag också lärt mig vad utmed planet innebär hehe. Förstod det inte riktigt i början men nu förstår jag det lite bättre. Okej jag hajar men tror du min professor hade förstått det med prickarna ("tagen i denna riktning", vi har inte sett det än eller denna metoden? Det make:ar sense också att vi inte har med normalkrafterna, dels för att de tar ut varandra och dels för att cos(90)=0.

Ja, din lärare har alldeles säkert sett beteckningen. Men om du vill vara extra tydlig kan du istället skriva i vilken riktning ekvationen projiceras. Andra vanliga sätt är att skriva

i $\hat{x}$ -led, i $\hat{y}$ -led

Eller i löptext, som "i radiell led", i "tangentiell led".

D4NIEL skrev:
Ja, din lärare har alldeles säkert sett beteckningen. Men om du vill vara extra tydlig kan du istället skriva i vilken riktning ekvationen projiceras. Andra vanliga sätt är att skriva

i $\hat{x}$ -led, i $\hat{y}$ -led

Eller i löptext, som "i radiell led", i "tangentiell led".

Ah okej, tack så mycket, jag lämnar det som det är med prickarna (fräckt)!

Tänk också på att centripetalkraften ska vara resultanten till de övriga krafterna precis som du säger i Edit 4 i ditt andra inlägg. Det är den som följer av $ma$ i $F=ma$ .

Så när du frilägger lådan får bara krafterna $N$ , $F_f$ och $mg$ vara med i friläggningsbilden. Centripetalkraften kommer automatiskt med när du ställer upp Newtons andra lag (genom accelerationen).

Om du behöver kan du rita extra bilder bredvid för att klura ut vilken vinkel accelerationen har vs planet och så vidare. Men försök hålla friläggningen så ren som möjligt, det har du nytta av senare!