Fritt fall med luftmotstånd - matte 5

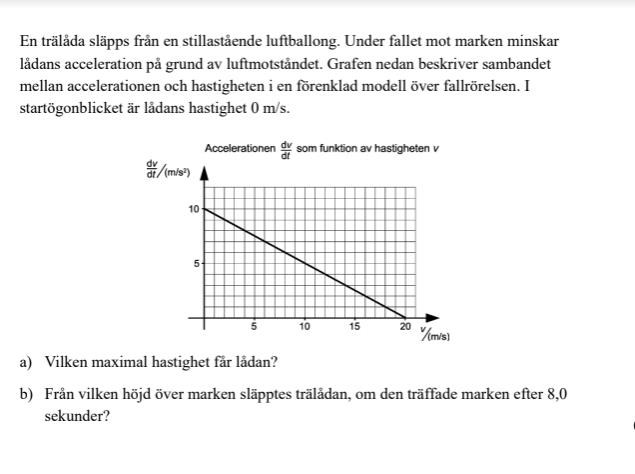
Du behöver inte veta massan för att lösa uppgiften. Du vet accelerationen som funktion av hastigheten så du kan ställa upp en differentialekvation och lösa den. Hjälp på vägen:

$\displaystyle h''\left(t\right)+\frac{1}{2}h'\left(t\right)=0$

Här har vi alltså att $h(t)$ är höjden som funktion av tiden. Från uppgiften har du  att $h(t=8)=0$ och $h'(0)=0$.

Min hjärna är helt blank när det gäller denna uppgift, skulle du kunna förklara steg för steg? 

Uppgift a)

Du kan enkelt se vad den maximala hastigheten blev direkt genom avläsning i grafen.

Uppgift b)

Jag får ursäkta men jag skrev helt fel i mitt tidigare svar. Du har att accelerationen beror av hastigheten enligt en linjär funktion nedan:

$\displaystyle a\left(v \right)=10-\frac{1}{2}v$

Där lutningen på den linjära funktionen bestäms från grafen enligt vad du lärde dig i Matte 2. Differentialekvationen blir:

$\displaystyle h''\left(t \right)+\frac{1}{2}h'\left(t \right)=10$

Denna typ av differentialekvation löser du genom att först lösa den homogena ekvationen (den där högerledet är noll). Detta gör du med den karakteristiska ekvationen som du kan läsa mer om här (länk):

$\displaystyle r^{2}+\frac{1}{2}r=0$

Denna ekvation har lösningen:

$\displaystyle r_{1}=0$ och $\displaystyle r_{2}=-0.5$

Vi får därmed följande lösning till den homogena differentialekvationen:

$\displaystyle h(t)=C_{1}e^{r_{1}t}+C_{2}e^{r_{2}t}$

$\displaystyle h(t)=C_{1}+C_{2}e^{-0.5t}$

För partikulärlösningen ansätter vi en linjär funktion (enkel konstant finns i homogena lösningen):

$\displaystyle h_{p}(t)=C_{3}t$

Detta ger direkt genom derivering att:

$\displaystyle h_{p}'(t)=C_{3}$

$\displaystyle h_{p}''(t)=0$

Således får vi vid instoppning i differentialekvationen:

$\displaystyle 0 + \frac{1}{2}C_{3}=10$

Vilket ger att $\displaystyle C_{3}=20$. Vi har därmed vår allmänna lösning som:

$\displaystyle h(t)=C_{1}+C_{2}e^{-0.5t} + 20t$

Vi vet från uppgiften att "I startögonblicket är lådans hastighet 0 m/s" vilket ger oss följande begynnelsevillkor:

$h'(0)=0$

Om vi för in detta villkor i vår deriverade allmänna lösning får vi:

$\displaystyle h'(t)=-0.5 \cdot C_{2}e^{-0.5t} + 20$

$\displaystyle h'(0)=-0.5 \cdot C_{2}+20=0$

Vilket naturligtvis ger att $C_{2} = 40$. Vi vet även från uppgiften att "...[lådan] träffade marken efter 8,0 sekunder" vilket ger följande redan nämnda randvillkor:

$h(t=8)=0$

Om vi för in detta villkor i vår uppdaterade allmänna lösning får vi:

$\displaystyle h(t)=C_{1}+ 40e^{-0.5t} + 20t$

$\displaystyle h(8)=C_{1}+ 40e^{-4} + 160=0$

Vilket ger $\displaystyle C_{1}=-160-40e^{-4}$ och vi får vår slutliga lösning som:

$\displaystyle h(t)= - 160 - 40e^{-4}+40e^{-0.5t} + 20t$

Vi får nu svaret som:

$\displaystyle h(0)= - 120- 40e^{-4}$ $m \approx -120.73$ $m$.

Märk väl att vi har definierat positiv riktning som nedåt och marken som noll vilket betyder att vi börjar vid en negativ höjd. Denna definition kommer från att accelerationen bestäms som positiv från grafen. Alltså är det riktiga svaret absolutbeloppet av ovan vilket blir:

$\displaystyle h(0) \approx 120.73$ $m$

Ebola skrev:

Uppgift a)

Du kan enkelt se vad den maximala hastigheten blev direkt genom avläsning i grafen.

Uppgift b)

Jag får ursäkta men jag skrev helt fel i mitt tidigare svar. Du har att accelerationen beror av hastigheten enligt en linjär funktion nedan:

$\displaystyle a\left(v \right)=10-\frac{1}{2}v$

Där lutningen på den linjära funktionen bestäms från grafen enligt vad du lärde dig i Matte 2. Differentialekvationen blir:

$\displaystyle h''\left(t \right)+\frac{1}{2}h'\left(t \right)=10$

Denna typ av differentialekvation löser du genom att först lösa den homogena ekvationen (den där högerledet är noll). Detta gör du med den karakteristiska ekvationen som du kan läsa mer om här (länk):

$\displaystyle r^{2}+\frac{1}{2}r=0$

Denna ekvation har lösningen:

$\displaystyle r_{1}=0$ och $\displaystyle r_{2}=-0.5$

Vi får därmed följande lösning till den homogena differentialekvationen:

$\displaystyle h(t)=C_{1}e^{r_{1}t}+C_{2}e^{r_{2}t}$

$\displaystyle h(t)=C_{1}+C_{2}e^{-0.5t}$

För partikulärlösningen ansätter vi en linjär funktion (enkel konstant finns i homogena lösningen):

$\displaystyle h_{p}(t)=C_{3}t$

Detta ger direkt genom derivering att:

$\displaystyle h_{p}'(t)=C_{3}$

$\displaystyle h_{p}''(t)=0$

Således får vi vid instoppning i differentialekvationen:

$\displaystyle 0 + \frac{1}{2}C_{3}=10$

Vilket ger att $\displaystyle C_{3}=20$. Vi har därmed vår allmänna lösning som:

$\displaystyle h(t)=C_{1}+C_{2}e^{-0.5t} + 20t$

Vi vet från uppgiften att "I startögonblicket är lådans hastighet 0 m/s" vilket ger oss följande begynnelsevillkor:

$h'(0)=0$

Om vi för in detta villkor i vår deriverade allmänna lösning får vi:

$\displaystyle h'(t)=-0.5 \cdot C_{2}e^{-0.5t} + 20$

$\displaystyle h'(0)=-0.5 \cdot C_{2}+20=0$

Vilket naturligtvis ger att $C_{2} = 40$. Vi vet även från uppgiften att "...[lådan] träffade marken efter 8,0 sekunder" vilket ger följande redan nämnda randvillkor:

$h(t=8)=0$

Om vi för in detta villkor i vår uppdaterade allmänna lösning får vi:

$\displaystyle h(t)=C_{1}+ 40e^{-0.5t} + 20t$

$\displaystyle h(8)=C_{1}+ 40e^{-4} + 160=0$

Vilket ger $\displaystyle C_{1}=-160-40e^{-4}$ och vi får vår slutliga lösning som:

$\displaystyle h(t)= - 160 - 40e^{-4}+40e^{-0.5t} + 20t$

Vi får nu svaret som:

$\displaystyle h(0)= - 120- 40e^{-4}$ $m \approx -120.73$ $m$.

Märk väl att vi har definierat positiv riktning som nedåt och marken som noll vilket betyder att vi börjar vid en negativ höjd. Denna definition kommer från att accelerationen bestäms som positiv från grafen. Alltså är det riktiga svaret absolutbeloppet av ovan vilket blir:

$\displaystyle h(0) \approx 120.73$ $m$

Tack så mycket, nu förstår jag!