Fröspridning matematik 5, problemlösning
Hej jag ska lösa denna uppgiften men har fastnat lite på hur jag ska göra för att få fram C och k. Diagrammet till är det jag gjort där jag endast satt in de värdena uppgiften gett mig.
Min första tanke var att jag kunde få fram C genom att sätta y(0)=462 men insåg att det står bara ett värde för y när y är något mellan 0-1 som den är 462. Har någon ett tips på hur jag kan göra för att få fram då antingen C eller k som en hjälp på vägen?
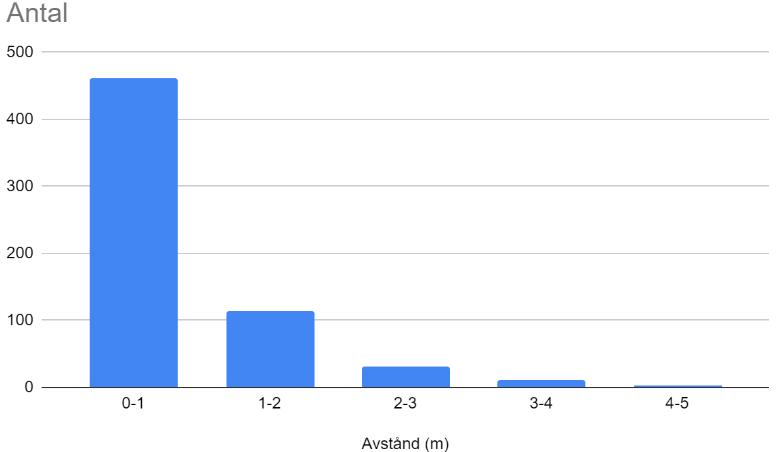ser med diagrammet att det är en exponentialfunktion som går mot 0 och detta får mig att tänka att k måste vara negativt (<0) men vet inte hur jag ska få fram varken k eller C när jag bara har värden som 0-1, 1-2 osv.
Tack på förhand!
Hög nivå på denna uppgift för att vara "matematik 5". Får du ta till vilka redskap du vill? Då kan du använda din grafräknare eller excel och göra en anpassning. Annars kan du göra en linjärisering som du kan läsa mer om hur man gör här:
http://www.math.chalmers.se/Math/Grundutb/CTH/Matlab/StudioALA/ht12/Linj_Newton.pdf
Tillägg: 4 maj 2022 18:46
Tänk på att punkten som innehar värdet är mittpunkten i varje intervall hos "histogramet". Alltså att dina punkter är:
x y
0.5 462
1.5 115
2.5 31
etc.
Ahh okej, tack så mycket! Kan jag använda mig av y(0.5)=462 och y(1.5)=115 då tex för att få fram ett C och ett k-värde algebraiskt eller kan jag inte anta att det just är 0.5 och 1.5 som har dem värdena?
Algebraiskt kommer ge felaktigt värde. Du måste använda all tillgänglig data. Bästa metoden i detta fall är då minstakvadrat-metoden. Jag kan inte riktigt ge någon rekommendation om jag inte vet vad som är tillåtet. Får du använda vilket redskap du vill? Grafräknare, excel, geogebra, etc.
Tillägg: 4 maj 2022 20:18
Här gjorde jag en trendlinje i Google kalkylark (gratis online-verktyg) vilket gav:
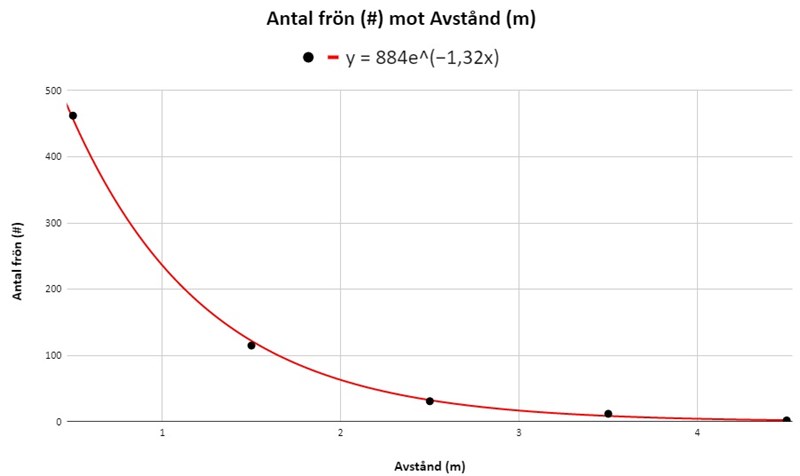
Vi får anpassningen:
Ja förlåt, alla hjälpmedel är tillgängliga! Okej tack så mycket!
Hej igen, har fortsatt arbeta med uppgiften nu och är på sista delen. Kollade på en video för att förstå partiell integration och kom fram till att V=0,7575... Vet inte om detta svaret är rätt och vet inte heller hur jag skulle förklara vad väntevärdet beskriver så har svårt att förstå om det jag fått är rimligt. Någon som vet?
Svaret är rätt.
Läs på om väntevärde och fundera. Tänk på att det är kontinuerliga slumpvariabeln som du beräknat ett väntevärde för. Alltså, det förväntade värdet är , vad kan det betyda?
SaintVenant skrev:Svaret är rätt.
Läs på om väntevärde och fundera. Tänk på att det är kontinuerliga slumpvariabeln som du beräknat ett väntevärde för. Alltså, det förväntade värdet är , vad kan det betyda?
Vad är väntevärdet i den här uppgiften?
