6 svar

240 visningar

Ygolopot behöver inte mer hjälp

Fundamental Theorem of Finit Abelian Groups

Hej, en kort fråga om följande sats:

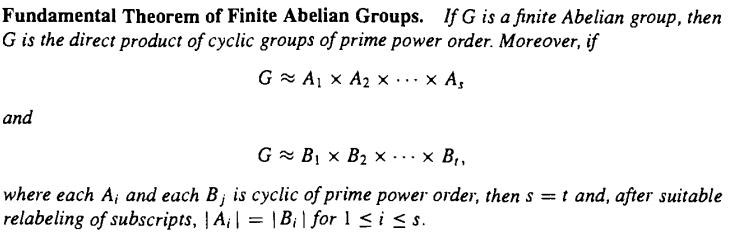
Här skriver man att: "then G is the direct product of cyclic groups of prime orders"

Jag tolkar det som att man menar att G är lika med gruppen som utgörs av direktprodukten är isomorfa. Menar man verkligen detta?

Nu har man inte formellt definierat direktprodukten i texten mer än att ange ett Theorem som visar varför det är en grupp med avseende på en viss operation men man skriver att direktprodukten är:

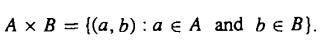
Jag har lite svårt att förstå hur ett element c i G kan vara lika med (a,b) i AxB. Jag vet ju i och för sig inte heller vad det innebär riktigt att två grupper är lika: samma element och samma operation?

Boken jag följer är:

https://sgheningputri.files.wordpress.com/2014/12/durbin-modern-algebra.pdf

Mvh

Nä två grupper är lika om det finns en isomorfi mellan dem.

Satsen säger att varje ändlig abelsk grupp är isomorf med en direkt produkt av cykliska grupper av primtalsordning.

Exempelvis Z6 ~Z2*Z3.

Testa detta exempel. Det vill säga skriv upp gruppernas grupptabeller och se om du kan se isomorfin.

Visa spoiler

Testa funktionen som ges av

(1,1)->1

(0,2)->2

(1,0)->3

(0,1)->4

(1,2)->5

(0,0)->0

Aha okej då förstår jag tack!

Om jag får lov att ställa en följdfråga, så förstår jag inte riktigt följande konstaterande efter satsen:

"Because each cyclic group of prime power order $p^{k}$ is isomorphic to $ℤ_{p^{k}}$ we can use... "

Alltså dom skriver: because each, alltså varje enskild(?) cyklisk grupp av prime power order är alltså isomorf till gruppen $ℤ_{p^{k}}$ av samma order. Varifrån får dom detta? Du hjälpte mig i en tidigare tråd om en annan sats men den behandlade ju fallet när vi har primtalsordning och cyklisk grupp, så det kan inte vara mot bakgrund av detta som man kan dra denna slutsats? För i så fall förstår jag det som att det är en direkt konsekvens av den sats jag frågade om här och jag förstår inte riktigt den kopplingen. Bild på texten i sin helhet nedan:

Jo alltså om p är primtal så är alla grupper av ordning p isomorfa, som vi diskuterade i den andra tråden.

Det är inte sant om ordningen är p^k, exempelvis är inte Klein Viergruppe isomorf med Z_4.

Däremot har vi ju här ytterligare ett antagande nämligen "each cyclic group of prime power order".

Här har det egentligen inget att göra med prime power order, två cykliska grupper som är lika stora är isomorfa.

Tänk på det utifrån vad vi diskuterade i den andra tråden, alltså att man kan hitta isomorfier genom att mappa generatorer på varandra.

Så om vi har två cyckliska grupper G och H av ordning n. Att de är cykliska betyder att de genereras av ett enda element, säg g respektive h. Funktionen som avbildar g på h, g^2 på h^2, g^3 på h^3... g^n på h^n är då en isomorfi, man kan visa det enkelt.

Så två lika stora cykliska grupper är isomorfa, rent allmänt. Så i specialfallet: en cyklisk grupp av primtalspotensordning så är den isomorf med Z_(p^k).

En cyklisk grupp $G$ av ordning $n$ är alltid isomorf med $\mathbb{Z}_n$ .

Att $G$ är cyklisk av ordning $n$ betyder att det finns något $a\in G$ sådant att $G$ kan skrivas på formen $G=\{1,a,a^2,\ldots,a^{n-1}\}$ , och det visar sig att vi får en isomorfi $\varphi:\mathbb{Z}_n\to G$ genom att mappa $[k]\mapsto a^k$ .

Övning: Att detta verkligen är en gruppisomorfi är nog intuititivt ganska uppenbart (båda grupperna har samma typ av "klockaritmetik-liknande" struktur), men det kan nog ändå vara en bra att övertyga sig lite mer formellt om att $\varphi$ verkligen är en väldefinierad gruppisomorfi.

Visa spoiler

Väldefinierad: Om $[k]=[k']$ så betyder det att $k'=k+mn$ för något $m\in\mathbb{Z}$ , vilket ger $\varphi([k'])=\varphi([k+mn])=a^{k+mn}=a^k\cdot (a^{n})^m=a^k\cdot 1^m=a^k=\varphi([k])$ .

Grupphomomorfi: $\varphi([k]+[\ell])=\varphi([k+\ell])=a^{k+\ell}=a^k\cdot a^{\ell}=\varphi([k])\cdot\varphi([\ell])$ .

Surjektiv: Uppenbart!

Injektiv: Kom ihåg att det räcker att visa att kärnan är trivial för att dra slutsatsen att en grupphomomorfi är injektiv. Notera att $\varphi([k])=1$ betyder att $a^k=1$ , vilket i sin tur måste betyda att $k$ är en multipel av $n$ , vilket i sin tur medför att $[k]=[0]$ .

Ny övning: Jämför vad vi gjorde här ovan, med beviset av den fundamentala homomorfisatsen (Sats 23.1) i din bok. Det visar sig att boken nästan exakt samma arbete när de visar den satsen, fast i större generalitet! Vi kan därför använda satsen för att ge ett mer kortfattat bevis för att vår avbildning $\varphi$ är en isomorfi. Hur?

Edit: Smutsmunnen var "lite" snabbare än mig! ^_^

Felpost

Glömde svara här, men stort tack för hjälpen båda två! Har hjälpt mig mycket :)

Svara

Visa senaste svar