Egenskaper för funktion i Z(4711)
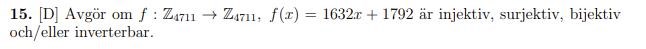
Jag har försökt tolka facit på denna uppgiften men försöker förstå varför man tar sgd(1632, 4711) = 1
och på så sätt kan säga att 1632 är inverterbar i
Vad säger största gemensamma nämnaren mellan mod 4711 och 1632 om funktionens inverterbarhet?
Flyttade tråden från Ma5 till ma/Uni /Smaragdalena, moderator
Du kan använda Euklides algoritm! Om du skriver upp alla stegen som leder fram till slutsatsen , så kan du genom att subsitituera och jobba "baklänges" uttrycka den största gemensamma delaren som en linjärkombination av och . Mer precist kan du hitta heltalskoefficienter , sådana att
Att göra detta i praktiken och räkna ut fungerande värden på och kan vara lite bökigt och tidsödande, men ofta (till exempel i det här fallet) kommer man undan med att veta att det går*.
Mod 4711 ger likheten ovan nämligen attt
men , så vi får
dvs. är inverterbart in .
* Detta faktum är faktiskt så användbart att man har gett det namnet Bézouts identitet. Ni har kanske redan gått igenom detta i din kurs - annars kommer du säkert stöta på det om du läser mer talteori efter gymnasiet!
Nu vet vi att har en multiplikativ invers i . Om vi vill kan vi fortsätta kalla den , eller så införa vi den mer praktiska symbolen .
Då kan vi börja undersöka hur vår funktion fungerar.
Låt oss börja med att kolla injektivitet. Det klassiska sättet att visa detta på är att anta att två inputs ger samma output, och sedan visa att den enda möjligheten då är att dessa inputs var lika med varandra.
Vi antar med andra ord att .
Det innebär att .
Kan du utifrån detta visa att måste gälla?
När du har klarat detta kan du gå vidare och visa surjektivitet.
Kanske kan du till och med hitta en explicit invers ?
Om du kör fast är det bara att säga till, så hjälper jag eller någon annan här gärna dig vidare!
Sidenote: Jag använder hakparenteser för att indikera att vi jobbar i talsystemet i stället för de vanliga heltalen . Om detta känns som en förvirrande notation kan du bara ignorera hakparentserna.
Jag följer typ med på vad du säger utöver det första (haha)
Hur förstår jag att jag ska kolla på sgd(1632, 4711) (jag hade alltså sett detta från facit), detta är första gången jag ser moduloräkning i en funktion.
Jag vet att vi tidigare löst genom att skriva om till och sedan gjort Euklides osv.
har det NÅGOT med detta att göra?
Vi har jobbat med Bezouts identitet, tror våran lärare kallade den extended euclidean algorithm, men det verkar inte som att du använder den för att lösa denna uppgift alls?
Om man börjar med att fundera på vad injektivitet, surjektivitet och inverterbarhet innebär (ungefär så som jag gjorde i mitt andra inlägg här ovan), så inser man ganska snabbt att detta kokar ner till inverterbarhet av i .
Det klassiska sättet att kolla om en sådan multiplikativ invers finns - och vid behov beräkna den - är just med Euklides algoritm. Generellt gäller att har en multiplikativ invers i om och endast om Euklides algoritm ger , och vill vi hitta inversen kan vi använda the extended Euclidean algoritm (det jag kallar "arbeta baklänges") för att hitta inversen.
I detta falllet gäller , så har en multiplikativ invers. Detta räcker för att visa att funktionen är både injektiv och surjektiv, och därmed även inverterbar. (Säg till om du behöver hjälp med att visa detta!)
Men - om vi vill hitta en explicit invers till funktionen så behöver vi bestämma den multiplikativa inversen för . Med våran extended Euclidean algorithm får vi fram att , vilket ger , så tydligen är .
(Tycker vi negativa tal är jobbigt kan vi så klart addera med , så ar tt vi i stället får .)
Hjälpte detta? Ser du vad inversen till funktionen blir nu? ^_^
Maals skrev:Jag vet att vi tidigare löst genom att skriva om till och sedan gjort Euklides osv.
har det NÅGOT med detta att göra?
Ohja! Att lösa ekvationen kokar också ner till att bestämma .
Tricket är precis som du skriver att notera att gäller om och endast om för något , dvs. om och endast om den diofantiska ekvationen har lösningar. Och som du säkert vet har den det om och endast om är en multipel av , och vill man hitta lösningarna kan man använda Euklides baklänges!
Notera speciellt att detta innebär att är lösbar för alla högerled om och endast om . (Vilket är ekvivalent med att har en multiplikativ invers i .)
Om vi vill så skulle vi kunna använda detta för att visa att vår funktion är surjektiv.
Det vi behöver visa är att för varje så finns det ett sådant att , dvs. vi behöver visa att ekvationen har en lösning för alla .
Jag skulle resoenera på följande sätt, utan att explicit referera till kongruenser eller det vi sa här ovanför om diofantiska ekvationer:
Visa spoiler
Eftersom vi vet att och att därför har en multiplikativ invers, så är detta enkelt. Det vanliga ekvationslösningstänktet från högstadiet ger
dvs. det finns en lösning!
Men om man gillar kongruenstecken och diofantiska ekvationer kan man i stället uttrycka sig så här:
Vi vill visa att ekvationen
har en lösning för alla , eller, ekvivalent, att ekvationen
har en lösning för alla , dvs. för alla möjliga värden av högerledet.
Och det har den ju (om vi följer resonemanget i början av inlägget), just eftersom .
Vill tacka för dina grymma svar!
Om jag förstått det hela rätt så är det viktiga att kolla på variabelns koefficient, alltså 1632 och om den är inverterar i så är funktionen också det, oavsett konstanten 1792?
Hur skulle det vara utifall vi hade flera variabler t.ex. ?
Här kan jag ju inte endast kolla att sgd(1721, 4711)=1 eftersom att jag har en andra variabel , eller..?
Maals skrev:Om jag förstått det hela rätt så är det viktiga att kolla på variabelns koefficient, alltså 1632 och om den är inverterar i så är funktionen också det, oavsett konstanten 1792?
Precis så är det!
Man kan se det som att en funktion (där är vilken så kallad ring som helst, t.ex. , ellöer ) på formen är en sammansättning av två "delfunktioner":
- Först gör vi en skalning: med .
- Sedan gör vi en translation: med .
En sådan translation är alltid inverterbar (eftersom den kan "göras ogjord" genom att subtrahera med ) så det som avgör om funktionen är inverterbar är skalningsfunktionen . Och den är inverterbar om och endast om skalfaktorn har en multiplikativ invers i .
Några exempel på detta (skissa gärna graferna, så att du får en känsla för hur de ser ut!):
Funktionen med är...
Visa spoiler
...inte inverterbar, eftersom det inte finns någon multiplikativ invers till skalfaktorn 2 i . (Den här funktionen missar alla jämna tal i målmängden, så den är inte surjektiv!)Funktionen med är...
Visa spoiler
...däremot inverterbar, eftersom skalfaktorn har sig själv som multiplikativ invers.Funktionen med är...
Visa spoiler
...också inverterbar, eftersom skalfaktorn 2 har en multiplikativ invers i .Funktionen med är...
Visa spoiler
...inte inverterbar, eftersom skalfaktorn saknar multiplikativ invers i . (Om man inte ser det direkt så kan man se det genom att .)Speciellt är den här funktionen inte surjektiv, eftersom den bara träffar elementen , och i målmängden.
Den är inte heller injektiv, eftersom bland annat .
Funktionen med är...
Visa spoiler
...inverterbar, eftersom skalfaktorn har en multiplikativ invers i . (Detta kan vi återigen se med Euklides algoritm, som även talar om att inversen är , om vi inte såg det direkt.)En följdfråga om du vill fundera mer på detta:
Kan du ge ett förslag på en skalfaktor som inte ger inverterbar funktion ?
Är detta verkligen Ma5? Det liknar ingenting som finns i den Ma5-bok som jag använder. /moderator
Maals skrev:Hur skulle det vara utifall vi hade flera variabler t.ex. i ?
En utmärkt fråga! ^_^
Tyvärr har talteori aldrig varit min starkaste sida, så jag kommer nog inte kunna göra detta full rättvisa eller förklara det på något superpedagogiskt sätt, utan vi får hoppas att någon annan här på forumet har bättre koll och kan hoppa in och hjälpa oss!
Men tills dess kan jag säga följande:
När vi lärde oss hantera andragradsfunktioner i Matematik 2 var tricket att kvadratkomplettera. Har vi en funktion med så är det mycket enklare att dra slutsatser om hur den kommer bete sig om vi skriver om den till
.
Detta kan vi försöka göra med andragradsfunktioner i också. Grunden till allt detta är ju till syvene och sist kvadreringsregeln, och den gäller lika bra i . Det enda problemet är att man får se upp med "division med 2". Om har en multiplikativ invers i så är detta inget problem, men för jämna kommer detta inte fungera, och då är man hänvisad till andra metoder...
Vi bortser för stunden även från att det kan finnas koefficienter framför andragradstermen.
Låt oss prova att kvadratkomplettera i ditt exempel: med .
Vi börjar med att konstatera att den multiplikativa inversen till är (detta kan du komma fram till med Euklides algoritm). Vi får nu att motsvarigheten till blir . Alltså gäller
.
Motsvarigheten till blir , så vi kan skriva
,
vilket med kvadreringsregeln baklänges ger
,
det vill säga
.
Detta är användbart på många sätt. Vill vi till exempel kolla om funktionen har några nollställen, så får vi ekvationen
Det betyder att vi får en lösning , för varje kvadratrot av (varje element sådant att ).
Men hur drar man egentligen roten ur något i ? Det är dessvärre en lång historia, som jag inte behärskar till fullo, men några nyckelord är kinesiska restsatsen, Lagrange-symboler och kvadratiska rester (eng. quadratic residues), som någon annan gärna får redogöra mer utförligt för.
Men det jag kan göra är att (försöka) förklara hur man kan komma fram till att inte har några kvadratrötter i .
Om man jobbar i för något primtal så kan man undersöka huruvida det finns några kvadratrötter med något som kallas för Eulers kriterium, men tyvärr är inget primtal...
Lyckligtvis visar det sig dock att man kan analysera varje primtalsfaktor för sig (men om vi har fler än en primtalsfaktor av samma sort blir det stökigare). Det gäller nämligen att om det finns sådant att , så måste både och gälla samtidigt. Ser du varför?
Visa spoiler
Låt och vara primtal sådana att . Detta är ekvivalent med att vilket i sin tur är ekvivalent med att och , dvs. och .
Låt oss nu studera dessa båda kongruenser var för sig:
- För behöver vi inte använda Eulers kriterium, eftersom , så kongruensen lyder helt enkelt som in sin tur är ekvivalent med och alltså löses av alla multiplar av 7.
- För kan vi enkelt konstatera att är relativt primt med , och att (här får man nog använda en miniräknare!), vilket enligt Eulers kriterium betyder att saknar lösningar.
Från detta drar vi slutsatsen att saknar kvadratrötter i , och därför också att får andragradsfunktion saknar nollställen. Speciellt betyder detta att funktionen inte är surjektiv, och att den därför inte heller kan vara inverterbar.
Och det är precis detta som inverterbarhet för andragradare i en generell ring kokar ner till generellt, förutsatt att har en multiplikativ invers så att man lyckas kvadratkomplettera funktionen till formen . Då kan funktionen precis som innan delas upp i delfunktioner:
- Först utför vi en translation: addition med .
- Sedan kvadrerar vi.
- Till sist translaterar vi igen: addition med .
Eftersom translationerna så klart är inverterbara, så hänger allt kvadreringen. Om kvadrering är injektivt i ringen vi jobbar i, så blir alla kvadratkompletterbara andragradare injektiva; om kvadreringen är surjektivt i ringen vi jobbar i, så blir alla kvadratkompletteringsbara andragradare surjektiva.
I såg vi precis att kvadrering inte är surjektivt, eftersom bland annat elementet saknade kvadratrot. Vi kan också enkelt se att kvadrering misslyckas med att vara injektivt, eftersom samtidigt som .
(Detta gäller för övigt även generellt: Kvadrering misslyckas alltid med att vara injektivt i för alla utom 2, eftersom det då gäller att , men likväl att och .)
Strök (på Oggihs uppmaning) bort några ord som inte borde vara där /Smaragdalena, moderator



