Funktioner

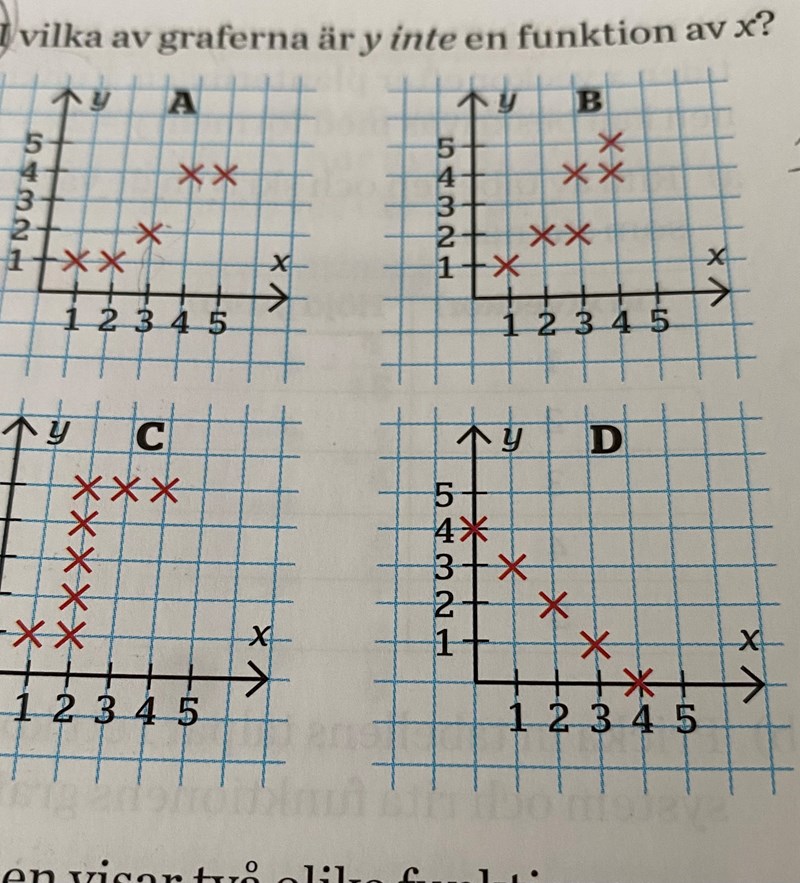
Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Darth Vader skrev:

Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Vad är funktionen? 

Ha en fin dag skrev:

Darth Vader skrev:

Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Vad är funktionen? 

I A så är funktionen $y=f(x)$ sådan att $f(1)=1$, $f(2)=1$, $f(3)=2$, $f(4)=4$ och $f(5)=4$. Observera att varje $x$ går mot exakt ett $y$ här.

Darth Vader skrev:

Ha en fin dag skrev:

Visa föregående citat

Darth Vader skrev:

Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Vad är funktionen? 

I A så är funktionen $y=f(x)$ sådan att $f(1)=1$, $f(2)=1$, $f(3)=2$, $f(4)=4$ och $f(5)=4$. Observera att varje $x$ går mot exakt ett $y$ här.

Vad är f… (Har precis börjat med funktioner så har verkligen ingen koll på någonting) 

Ha en fin dag skrev:

Darth Vader skrev:

Visa föregående citat

Ha en fin dag skrev:

Darth Vader skrev:

Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Vad är funktionen? 

I A så är funktionen $y=f(x)$ sådan att $f(1)=1$, $f(2)=1$, $f(3)=2$, $f(4)=4$ och $f(5)=4$. Observera att varje $x$ går mot exakt ett $y$ här.

Vad är f… (Har precis börjat med funktioner så har verkligen ingen koll på någonting) 

$f$ är funktionen du uträttar. Tänk till exempelvis en linje $y=2x+1$. Man kan också skriva denna som $y=f(x)$ så att $f(x)=2x+1$. $f$ är precis samma sak som $y$ bara en annan notation.

Formellt är $f$ en funktion som verkar mellan två mängder som tillordnar ett element från den ena till den andra. Om du exempelvis har mängderna $\{1,2,3\}$ och den andra mängden $\{a,b,c\}$ så kan jag om jag vill definiera en funktion $f$så att $f(1)=a$, $f(2)=c$ och $f(3)=b$.

Är du med?

Darth Vader skrev:

Ha en fin dag skrev:

Visa föregående citat

Darth Vader skrev:

Ha en fin dag skrev:

Visa föregående citat

Darth Vader skrev:

Om varje $x$ går mot exakt ett $y$ så finns det en funktion.

Vad är funktionen? 

I A så är funktionen $y=f(x)$ sådan att $f(1)=1$, $f(2)=1$, $f(3)=2$, $f(4)=4$ och $f(5)=4$. Observera att varje $x$ går mot exakt ett $y$ här.

Vad är f… (Har precis börjat med funktioner så har verkligen ingen koll på någonting) 

$f$ är funktionen du uträttar. Tänk till exempelvis en linje $y=2x+1$. Man kan också skriva denna som $y=f(x)$ så att $f(x)=2x+1$. $f$ är precis samma sak som $y$ bara en annan notation.

Formellt är $f$ en funktion som verkar mellan två mängder som tillordnar ett element från den ena till den andra. Om du exempelvis har mängderna $\{1,2,3\}$ och den andra mängden $\{a,b,c\}$ så kan jag om jag vill definiera en funktion $f$så att $f(1)=a$, $f(2)=c$ och $f(3)=b$.

Är du med?

Om man tar det ovanstående exemplet igen där $y=f(x)=2x+1$ så skulle jag exempelvis sätta $f(1)=2 \cdot 1 + 1=3$, $f(2)=2 \cdot 2 + 1=5$, $f(\pi)=2 \cdot \pi + 1 = 2 \pi + 1$ osv. Här är mängderna bara den reella tallinjen, eller $\mathbb{R}$ som den också kallas, respektive.

Om något x-värde kan ge två (eller flera) y-värden så är det INTE en funktion.