Funktioners egenskaper och formler

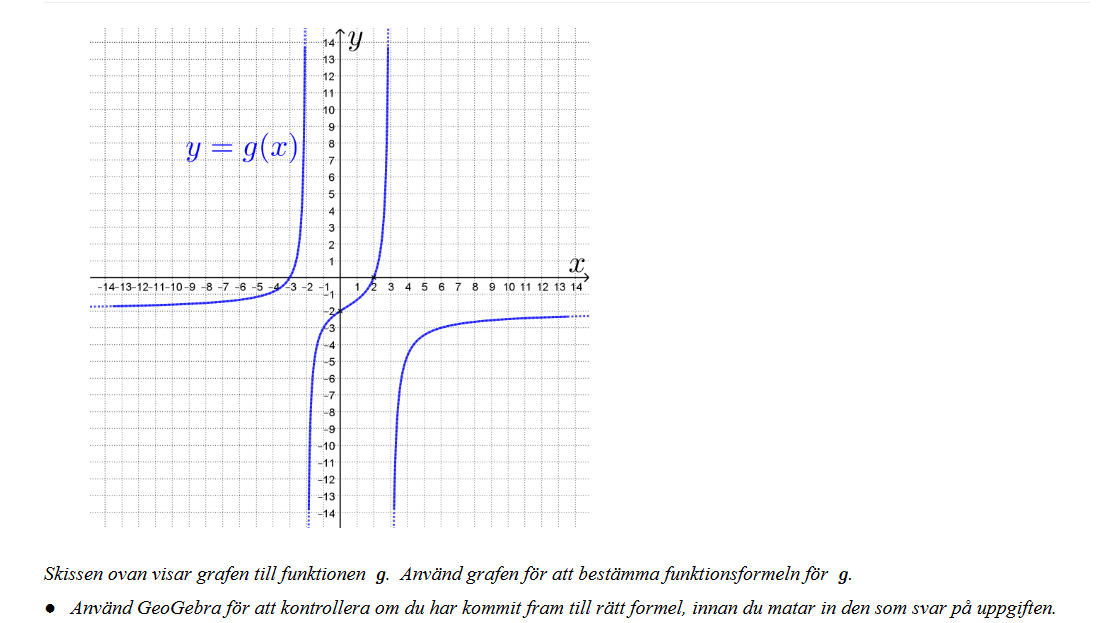
Eftersom grafen ser ut så här tänkte jag att funktionen måste vara en kvot. Jag började med att bestämma nämnaren genom att hitta de lodräta assymptoterna.

Vi ser att grafen blir närmare och närmare till x=-2 och x=3 vilket innebär att funktionen inte är definerat för dessa x-värden. Detta innebär att nämnaren måste vara: $(x + 2) (x - 3)$ eftersom x-värden -2 och 3 gör att nämnaren blir 0 vilket inte är definerat.

Jag bestämde därefter den vågräta asyymptoten. Vi ser att g(x) närmar sig mot -2 när x går mot |oändligheten|. $g (x) \to - 2 d å x \to \pm \infty$

Men jag vet inte nu hur jag ska koppla ihop dessa och bestämma täljaren och även dess grad.

Det var bra start!

Säg att nämnaren verkligen är $(x+2)(x-3)=x^2-x-6$ och att täljaren också är ett polynom.

Vad blir gradtalet i täljaren?

Om grad(T) < grad(N), så har kurvan en vågrät asymptot som sammanfaller med $x$ -axeln. Detta stämmer inte, så man vet att täljaren inte kan vara bara en konstant och inte heller ett linjärt uttryck.

Om grad(T) = grad(N), så har kurvan en vågrät asymptot som inte sammanfaller med $x$ -axeln. Detta verkar lovande.

Om grad(T) > grad(N), så har kurvan en sned asymptot eller ingen asymptot alls. Detta stämmer alltså inte.

Slutsats: Det är en andragradare i täljaren.

Säg att $T = ax^2 + bx + c$ , där talen $a$ , $b$ och $c$ behöver bestämmas utifrån grafen.

Asymptot:

Vad är $\displaystyle\lim_{x\to\pm\infty} \dfrac{ax^2 + bx + c}{x^2-x-6}$ ? Detta skall bli $-2$ p.g.a. asymptoten $y=-2$ . (Härmed kommer du kunna ta fram $a$ )

Skärning med y-axeln:

Kurvan skär y-axeln i punkten (0, -2). Det innebär att $g(0) = -2$ , där $g\left(x\right) = \dfrac{ax^2 + bx + c}{x^2-x-6}$ . (Härmed kommer du kunna ta fram $c$ )

Skärning med x-axeln:

Kurvan skär x-axeln i punkten (2, 0). Det innebär att $g(2) = 0$ , där $g\left(x\right) = \dfrac{ax^2 + bx + c}{x^2-x-6}$ . (Härmed kommer du kunna ta fram $b$ )

Anmärkning:

Det syns i grafen att det finns en till skärning med x-axeln, nämligen (-3, 0), så $g(-3)=0$ ska vara uppfylld. Täljaren ska alltså ha två nollställen, x=2 och x=-3. Därmed kan täljaren skrivas i faktorform $g(x) = a (x-2)(x+3)$ , där värdet på $a$ bestämts m.h.a. asymptoten.

Svara