Funktionsgraf_2
Behöver vi hittar funktion av grafen ovan?
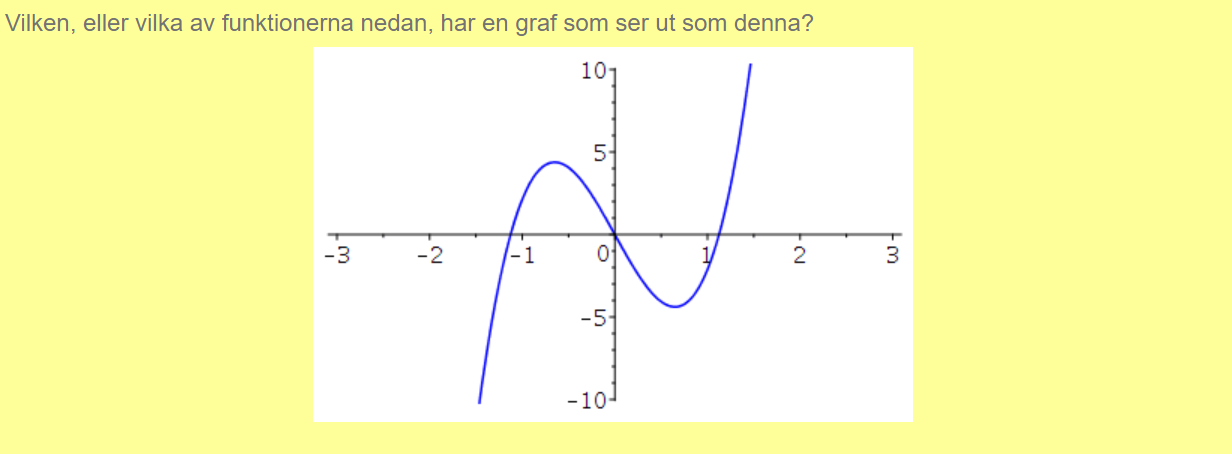

Nej, du behöver inte beräkna funktionen.
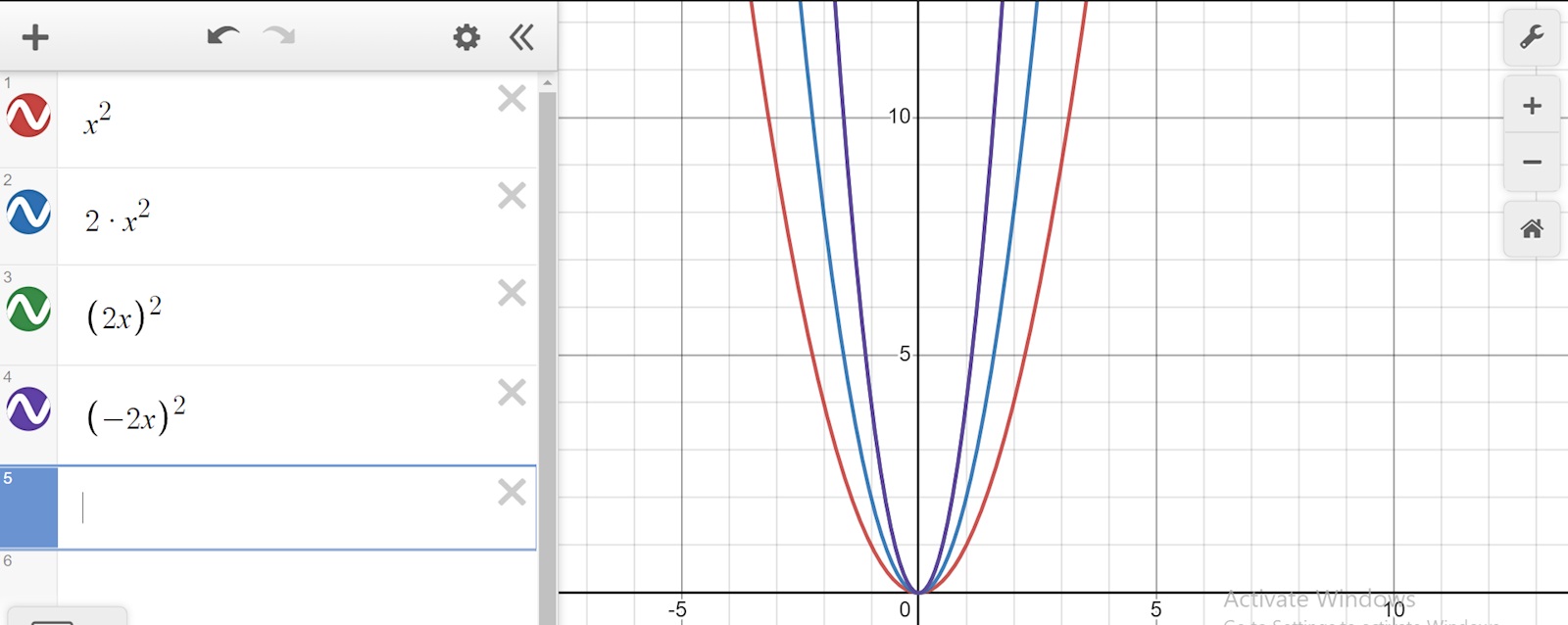
Låt f(x) vara x², prova nu skissa med desmos eller något liknande vad cx² gör, vad x²+d gör, vad f(x+a) gör osv. Så tror jag det klarnar.
Gjort ja rätt?
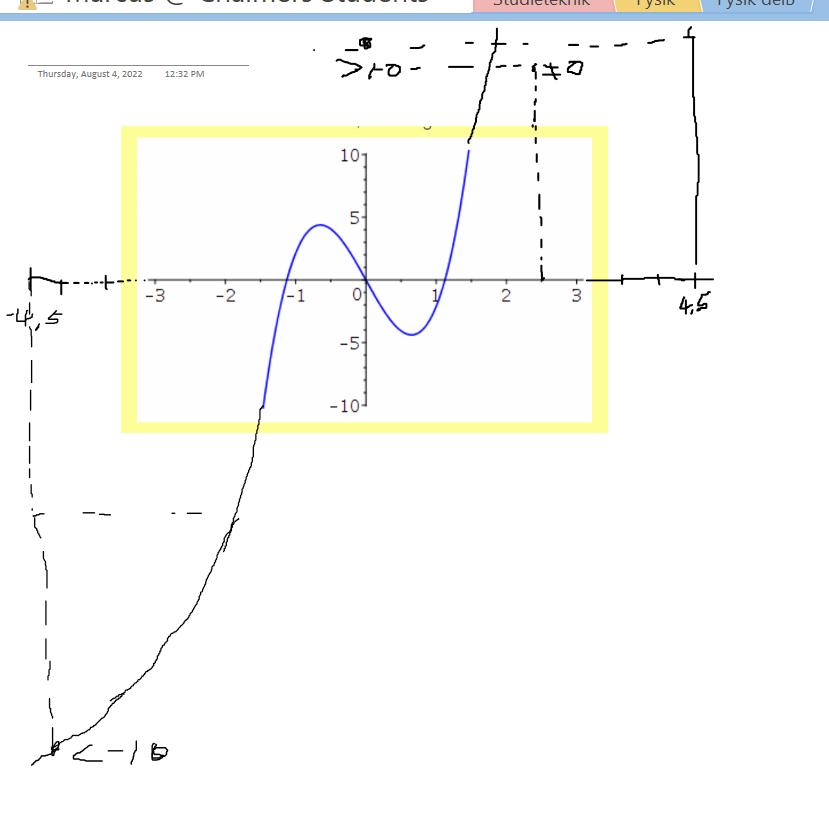
Du har skrivit att den nya grafen kan beskivas som 2 f(x), f(2x) och f(-2x).
Om x = 0 så är f(x) = 0 och detta stämmer för alla tre funktionerna du har skrivit.
Det ser ut som om x = 2,25 ungefär är ett annat nollställe för f(x). Då är f(2x) = f(4,5) = som är större än 10, men detta stämmer inte med den nya grafen. 2f(x) = 2f(2,25) = 2*0 = 0 som inte stämmer med den nya grafen. Och f(-2x) = f(-4,5) som gissningsvis är mindre än -10, och detta stämmer inte heller. Ingen av dina gissningar verkar alltså vara korrekt.
Men f(4.5) i den nya grafen är större än 10 !
f(2.25) i den nya grafen är inte 0 !
f(-2x) = f(-4.5) i den nya grafen är mindre än -10
Dracaena skrev:Nej, du behöver inte beräkna funktionen.
Låt f(x) vara x², prova nu skissa med desmos eller något liknande vad cx² gör, vad x²+d gör, vad f(x+a) gör osv. Så tror jag det klarnar.
Jag har prövat din metod, men det funkade inte så bra. Ingen av min gissning verkar vara korrekt.
Om vi låta f(x) lika med x^2 då är nya grafen samma som den gamla men bara smallare.
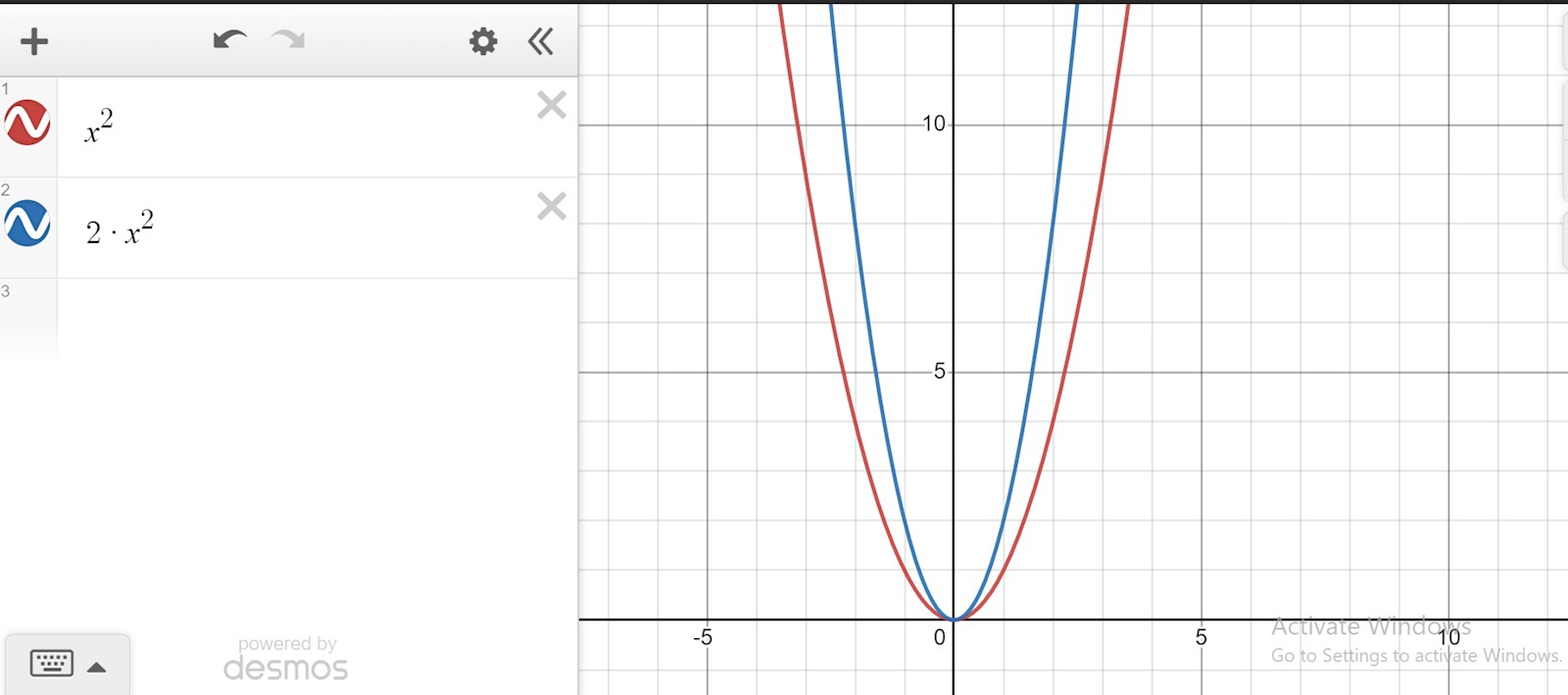
Smaragdalena skrev:Du har skrivit att den nya grafen kan beskivas som 2 f(x), f(2x) och f(-2x).
Om x = 0 så är f(x) = 0 och detta stämmer för alla tre funktionerna du har skrivit.
Det ser ut som om x = 2,25 ungefär är ett annat nollställe för f(x). Då är f(2x) = f(4,5) = som är större än 10, men detta stämmer inte med den nya grafen. 2f(x) = 2f(2,25) = 2*0 = 0 som inte stämmer med den nya grafen. Och f(-2x) = f(-4,5) som gissningsvis är mindre än -10, och detta stämmer inte heller. Ingen av dina gissningar verkar alltså vara korrekt.
Jag tror det är något fel här.
Jag tror att Smaragdalena har blandat ihop den nya och den gamla grafen.
Laguna skrev:Smaragdalena skrev:Du har skrivit att den nya grafen kan beskivas som 2 f(x), f(2x) och f(-2x).
Om x = 0 så är f(x) = 0 och detta stämmer för alla tre funktionerna du har skrivit.
Det ser ut som om x = 2,25 ungefär är ett annat nollställe för f(x). Då är f(2x) = f(4,5) = som är större än 10, men detta stämmer inte med den nya grafen. 2f(x) = 2f(2,25) = 2*0 = 0 som inte stämmer med den nya grafen. Och f(-2x) = f(-4,5) som gissningsvis är mindre än -10, och detta stämmer inte heller. Ingen av dina gissningar verkar alltså vara korrekt.
Jag tror det är något fel här.
Men håller du med min post på 12:30 ?
Jag håller med om det du skriver där, men vad är slutsatsen av det?
Laguna skrev:Jag håller med om det du skriver där, men vad är slutsatsen av det?
Min punkt är jag förstår fortfarande inte varför ja fick fel på denna svaret. Jag har följt metoden från början av tråden, alltså låtsas f(x)=x^2.
Marcus N skrev:
Min punkt är jag förstår fortfarande inte varför ja fick fel på denna svaret. Jag har följt metoden från början av tråden, alltså låtsas f(x)=x^2.
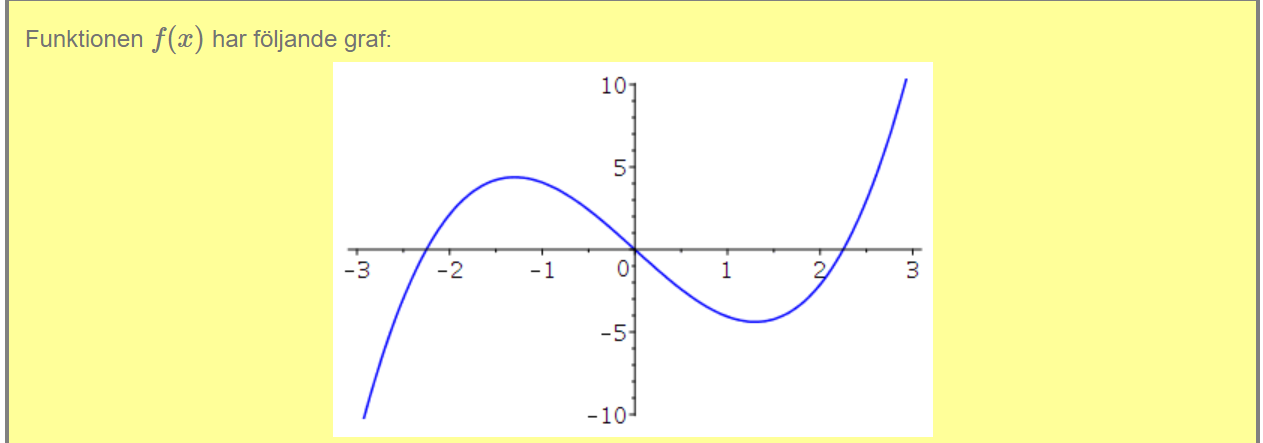
Titta på den första grafen.
Den har en maxpunkt vid ungefär , dvs .
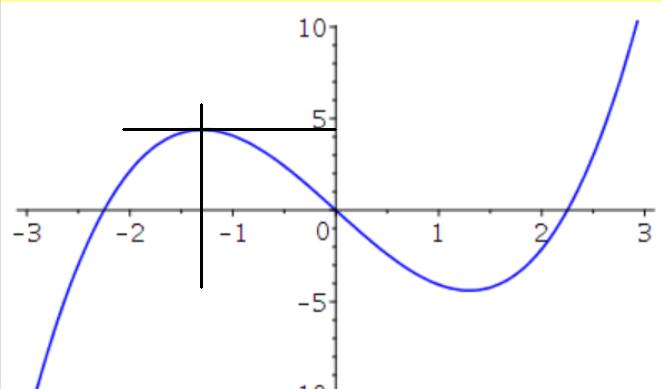
Om den andra grafen skulle vara så skulle den grafens höjd vid alltså vara , dvs ungefär . Det är den inte, så det alternativet måste vara fel.
Gör ett liknande resonemang med de andra två alternativen du har valt.