fx(lnx)/y <=> phi(lnx-mu/sigma)/y?

Hej! Jag sitter med följande uppgift, och jag har nästan rätt. Först uppgiften och facit:

(bilden blev lite avklippt, det ska stå $f_X(\ln y) \cdot \frac 1 y$)

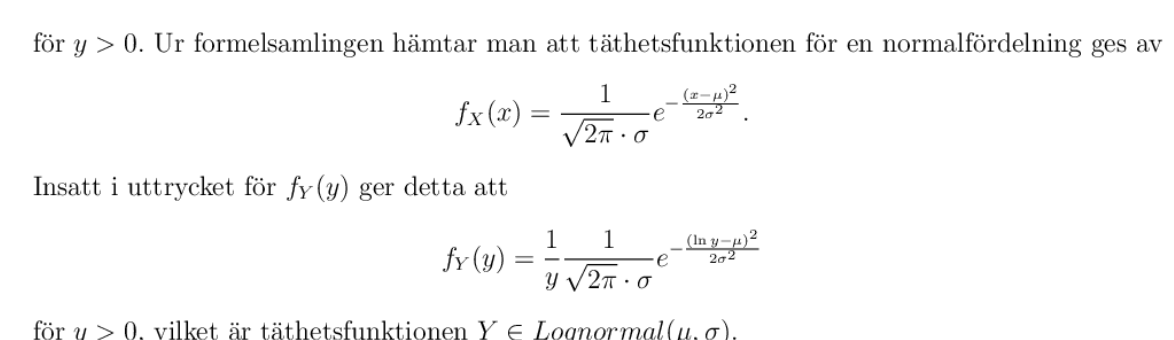
Jag tänkte - borde det inte gälla att

$f_X(x) = \varphi (\frac{x-\mu}{\sigma})$ där $\varphi$ är täthetsfunktionen för en $N(0,1)$-fördelad stokastisk variabel.

Därav, eftersom $f_X(\ln y) y^{-1}$ är täthetsfunktionen för Y:

$f_X(\ln y) = \varphi(\frac{\ln y-\mu}{\sigma})$

Grejen är dock att $\varphi$ är definierad enligt följande

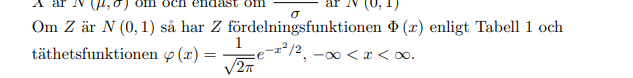
Så jag skulle då få  att fördelningen för Y är

$f_Y(y)=f_X(\ln y) y^{-1} =\frac {1}{\sqrt{2\pi}y}\exp(-\frac{1}{2} [\frac{\ln y- \mu}\sigma]^2)$

men grejen är, eftersom jag använde mig av $\varphi$ så finns inget $\sigma$ i nämnaren till $f_Y$, vilket jag skulle fått om jag inte gjorde om till $N(0,1)$. Jag är ute efter att hitta vad för "förbjudet antagande" jag gjort, så att jag inte gör om samma misstag igen.

Trevlig måndag och tack för svar!