Fysik fråga om stöt

Hej! För fullständigt elastiskt stöt gäller att den kinetiska energin såväl som rörelsemängden bevaras. Det finns regeln att v₁-v₂=-(u₁-u₂) och dess härledning kan jag. Men i min bok har man inte tagit upp denna formel utan den förutsätter att man ska använda ekvationssystem med bevarande av den kinetiska energin och rörelsemängden men det blir väldig lång matematik. Jag undrar vad orsaken kan vara till att man inte nämnt den, finns det vissa uppgifter då formeln inte fungerar och bör jag därför hålla mig till ekvationssystem?

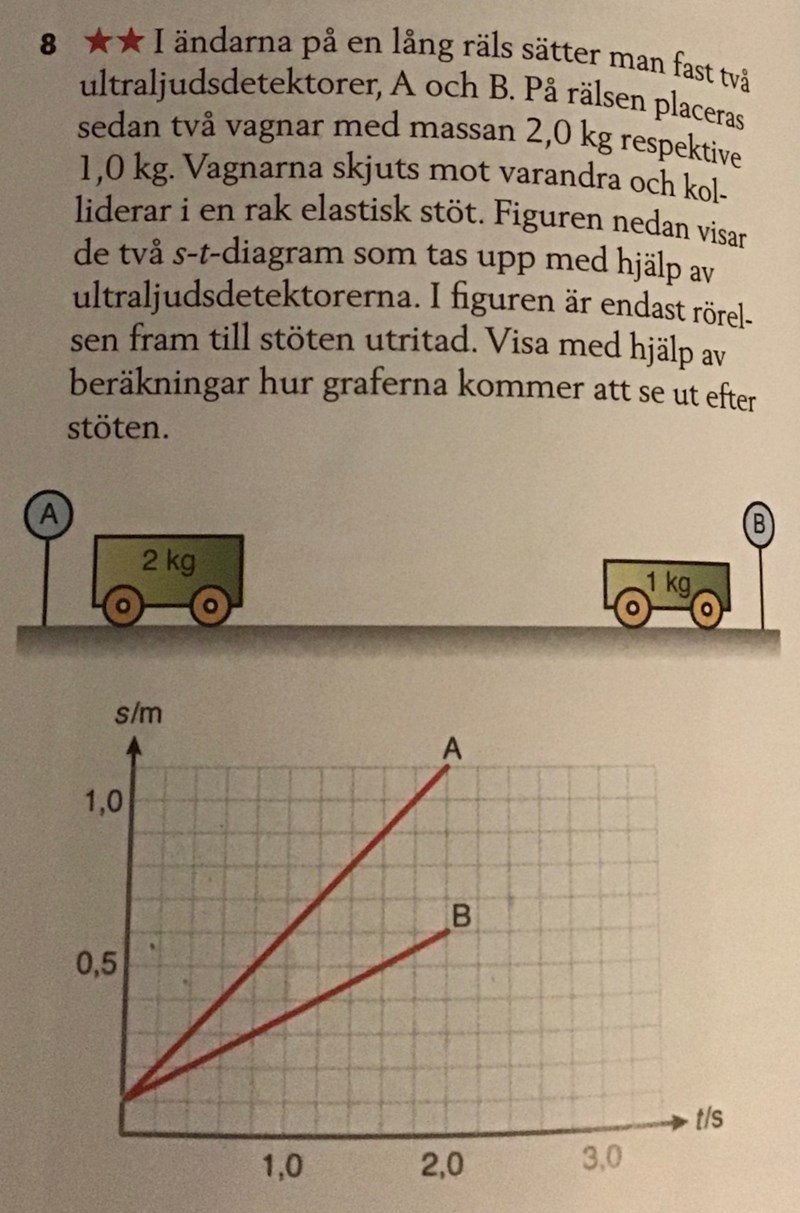
Till exempel denna fråga. Man får ju utifrån grafen hastigheterna före 0,5 m/s och -0,25 m/s

0,5-(-0,25)=-(v₁-v₂) ---> 0,75 = v₂-v₁

För just denna fråga står det på facit att hastigheterna efter är 0 m/s och 0,75 m/s vilket stämmer enligt ovan, men det är ju två okända variabler. Går det att lösa den trots allt eller bör jag då hålla mig till ekvationssystem?

Orsaken att den inte nämns är antagligen för att en elastisk stöt är egentligen ganska ointressant eftersom det aldrig sker i verkligheten. Således vill de lära dig träna på att räkna matematiken så att du kan hantera problem där kinetisk energi går förlorad.

Uppgiften du lagt upp en bild på har dubbla stjärnor vilket ska signalera att den är på mycket hög nivå. Hursomhelst, om du använder relationen för elastisk spegling så får du direkt:

$0.75 = u_{2} - u_{1}$

Du har en annan relation från rörelsemängdens bevarande som ger:

$m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2}$

Du har två ekvationer och två okända så du kan bestämma hastigheterna efter stöten.

Ebola skrev:
Orsaken att den inte nämns är antagligen för att en elastisk stöt är egentligen ganska ointressant eftersom det aldrig sker i verkligheten. Således vill de lära dig träna på att räkna matematiken så att du kan hantera problem där kinetisk energi går förlorad.
Uppgiften du lagt upp en bild på har dubbla stjärnor vilket ska signalera att den är på mycket hög nivå. Hursomhelst, om du använder relationen för elastisk spegling så får du direkt:
$0.75 = u_{2} - u_{1}$
Du har en annan relation från rörelsemängdens bevarande som ger:
$m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2}$
Du har två ekvationer och två okända så du kan bestämma hastigheterna efter stöten.

Okej, men ekvationen 0,75=u₂-u₂ är ju framtagen genom att ha använt både relationen om rörelsemängdens bevarande samt bevarandet av den kinetiska energin, kan man då ändå använda samma ekvation (som användes till den framtagna ekvationen) för att inkludera i ekvationssystemet och skulle det då gå lika bra att använda 0,75=u2-u2 och ekvationen om kinetiska energins bevarande (även om det blir krångligare)?

Leonhart skrev:
Okej, men ekvationen 0,75=u₂-u₂ är ju framtagen genom att ha använt både relationen om rörelsemängdens bevarande samt bevarandet av den kinetiska energin, kan man då ändå använda samma ekvation (som användes till den framtagna ekvationen) för att inkludera i ekvationssystemet

Din magkänsla pekar på något som är ganska intressant fast överkurs men du kan se det som att relationen för relativa hastigheter innehåller information både från rörelsemängden och rörelseenergins bevarande. För att få fram den har du nämligen dividerat ena ekvationen med den andra. Det är alltså en annan representation av hur variablerna relaterar till varandra men det är ingen ny information. Detta betyder att du kan kombinera din nya ekvation med vilken som helst av de två du formade den med.

Föreställ dig att vi har följande ekvationssystem:

$\{\begin{cases} (x + y) (x - y) = 6 \\ x + y = 2 \end{cases}$

Vi dividerar nu den första ekvationen med den andra:

$\frac{(x + y) (x - y)}{x + y} = \frac{6}{2} \Leftrightarrow x - y = 3$

Vi kan nu lösa ekvationssystemet enkelt och få:

$x = \frac{5}{2}; y = - \frac{1}{2}$

Det vi ser är att Ekvation 1 var:

$(E k v a t i o n 2) (E k v a t i o n 3) = 2 \times 3 = 6$

Alltså skulle vi kunna betrakta det som att vårt ursprungliga ekvationssystem egentligen bara bestod av Ekvation 2 och 3 som nedan:

$\{\begin{cases} x + y = 2 \\ x - y = 3 \end{cases}$

Eller som i ditt fall att vi egentligen hade:

$v_{1} - v_{2} = - (u_{1} - u_{2}) m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2}$

Inte så bra förklarat men jag försökte iallafall ;)

skulle det då gå lika bra att använda 0,75=u2-u2 och ekvationen om kinetiska energins bevarande (även om det blir krångligare)?

Ja.

Ebola skrev:
Leonhart skrev:
Okej, men ekvationen 0,75=u₂-u₂ är ju framtagen genom att ha använt både relationen om rörelsemängdens bevarande samt bevarandet av den kinetiska energin, kan man då ändå använda samma ekvation (som användes till den framtagna ekvationen) för att inkludera i ekvationssystemet
Din magkänsla pekar på något som är ganska intressant fast överkurs men du kan se det som att relationen för relativa hastigheter innehåller information både från rörelsemängden och rörelseenergins bevarande. För att få fram den har du nämligen dividerat ena ekvationen med den andra. Det är alltså en annan representation av hur variablerna relaterar till varandra men det är ingen ny information. Detta betyder att du kan kombinera din nya ekvation med vilken som helst av de två du formade den med.
Föreställ dig att vi har följande ekvationssystem:
$\{\begin{cases} (x + y) (x - y) = 6 \\ x + y = 2 \end{cases}$
Vi dividerar nu den första ekvationen med den andra:
$\frac{(x + y) (x - y)}{x + y} = \frac{6}{2} \Leftrightarrow x - y = 3$
Vi kan nu lösa ekvationssystemet enkelt och få:
$x = \frac{5}{2}; y = - \frac{1}{2}$
Det vi ser är att Ekvation 1 var:
$(E k v a t i o n 2) (E k v a t i o n 3) = 2 \times 3 = 6$
Alltså skulle vi kunna betrakta det som att vårt ursprungliga ekvationssystem egentligen bara bestod av Ekvation 2 och 3 som nedan:
$\{\begin{cases} x + y = 2 \\ x - y = 3 \end{cases}$
Eller som i ditt fall att vi egentligen hade:
$v_{1} - v_{2} = - (u_{1} - u_{2}) m_{1} v_{1} + m_{2} v_{2} = m_{1} u_{1} + m_{2} u_{2}$
Inte så bra förklarat men jag försökte iallafall ;)
skulle det då gå lika bra att använda 0,75=u2-u2 och ekvationen om kinetiska energins bevarande (även om det blir krångligare)?
Ja.

Tack så mycket, du förklarade jätte bra och det var väldigt intressant! Jag visste inte att man kunde dividera ekvationerna så då jag bara hållit mig till gauss- additions- och substitutionsmetoden, så det var mycket effektivare matematik än vad jag hade valt. Jag vill gärna gå till roten av hur allt föreligger sig med relationen mellan hastigheterna sig även om det är överkurs, vet du någon sida som går in på det?

Svara

Visa senaste svar