Fysik lab, mäta ström

Hej Pluggakuten.

Jag har nu en laboration som jag skulle vilja ha lite mer förklaring på.
Laborationen handlar om att mäta resistans och spänning, jag tänkte att jag börjar med den första deluppgiften som handlar om att mäta upp den totala resistansen. Jag har även fått fyra motstånd som jag mätt och fått att
r1 = 1ohm
r2 = 10ohm
r3 = 22ohm
r4 = 100ohm

Jag ska ta r2 och r3 i serie, och koppla r1 parallellt med båda två.
Och sedan göra samma sak, fast r4 koppat parallellt med båda två.
Jag har även fått med mig lite material som ett batteri och kopplingsdäck.

Men jag är lite osäker på hur dom menar när jag ska räkna ut total resistans, r2 och r3 är ju i serie, så det är bara att addera dom, men hur blir det med den som är parallellkopplad?
1/r1 = 1/r2 + 1/r3 eller vadå?

Tack.

rita upp att r2 och r3 är seriekopplade tillsammans samt parallellkopplade med r1

För seriekopplade resistorer är den totala resistansen som du säger r2 + r3 vilket ger dig 10+22=32 ohm

33ohm motstånd ligger nu parallellkopplat med 1hm motstånd (r1)

du har formeln för den totala resistansen vid parallellkoppling. Använd den

Det ser lite ut som att du inte har förstått vad som menas med ersättningsresistans (total resistans).

En ersättningsresistans har samma egenskaper som de resistanser som den ersätter. Om du t.ex. har en svart låda med 2 kontakter så kan du mäta resistansen mellan kontakterna. Då har du mätt en ersättningsresistans. Du har ingen aning om vad som finns i lådan. Det kan vara en hur komplicerad krets som helst men du har mätt upp den totala resistansen. Alltså en ersättningsresistans har samma effekt i en krets som allt (alla resistanser) har tillsammans.

Formeln som du har på slutet är en formel för hur man kan ersätta 2 parallellkopplade resistanser med 1 (ersättings)resistans. De 2 resistanserna här:

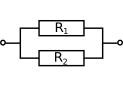
kan ersättas men en ersättningsresistans (total resistans) som kommer att ge en krets med samma egenskaper:

Men då måste du välja R så att formeln $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ är uppfylld. Annars har kretsen inte samma egenskaper längre.

Det framgår inte riktigt vad de frågar efter men jag gissar att i din laboration ska du bl.a. stegvis ersätta 2 resistanser med 1 tills att du har 1 total ersättningsresistans. D.v.s. 1 resistans som kan ersätta alla de andra utan att påverka kretsens egenskaper.

Ava.1 skrev:
rita upp att r2 och r3 är seriekopplade tillsammans samt parallellkopplade med r1

För seriekopplade resistorer är den totala resistansen som du säger r2 + r3 vilket ger dig 10+22=32 ohm

33ohm motstånd ligger nu parallellkopplat med 1hm motstånd (r1)

du har formeln för den totala resistansen vid parallellkoppling. Använd den

Tack! Jag ska sedan räkna ut vilket motstånd som är mest dominant, eller vilken som bidrar mest till ersättningsresistansen.. Det logiska i mig säger att det är resistansen som har mest ohm i sig, men det känns inte riktigt som ett rätt svar..
Är det något jag missat?

Peter skrev:
Det ser lite ut som att du inte har förstått vad som menas med ersättningsresistans (total resistans).

En ersättningsresistans har samma egenskaper som de resistanser som den ersätter. Om du t.ex. har en svart låda med 2 kontakter så kan du mäta resistansen mellan kontakterna. Då har du mätt en ersättningsresistans. Du har ingen aning om vad som finns i lådan. Det kan vara en hur komplicerad krets som helst men du har mätt upp den totala resistansen. Alltså en ersättningsresistans har samma effekt i en krets som allt (alla resistanser) har tillsammans.

Formeln som du har på slutet är en formel för hur man kan ersätta 2 parallellkopplade resistanser med 1 (ersättings)resistans. De 2 resistanserna här:

kan ersättas men en ersättningsresistans (total resistans) som kommer att ge en krets med samma egenskaper:

Men då måste du välja R så att formeln $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ är uppfylld. Annars har kretsen inte samma egenskaper längre.

Det framgår inte riktigt vad de frågar efter men jag gissar att i din laboration ska du bl.a. stegvis ersätta 2 resistanser med 1 tills att du har 1 total ersättningsresistans. D.v.s. 1 resistans som kan ersätta alla de andra utan att påverka kretsens egenskaper.

Hej Peter!
Ja det löste sig, och du hade precis rätt! Jag håller på att klura på vilken resistor som bidrar mest till ersättningsresistansen, jag vill säga resistorn med det största värdet, dvs 100 ohm, men det känns inte riktigt rätt.. Är det något du skulle kunna ha en tanke på? Tack! :)

Va kul att det löste sig!

vilken resistor som bidrar mest till ersättningsresistansen

Det är ekvationerna för seriekoppling och parallellkoppling som avgör vad som bidrar mest. Allt beror på hur de är kopplade. När du ska beräkna ersättningsresistansen i en krets som i labben så är det säkrast att ta ett steg i taget. Om man har något som ser ut så här:

så börjar man med att beräkna ersättningsresistansen för ovalen med formeln för parallellkoppling. Då får man:

där R uppfyller $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ . Sen har man en enkel seriekoppling och det är bara att addera resistanserna. Om man har något mer komplicerat:

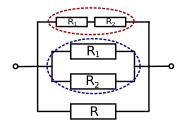
så beräknar man först ersättningsresistanserna för ovalerna och sen har man en parallellkoppling med 3 resistorer. Den totala resistansen kan man då räkna ut med

$\frac{1}{R_{t o t}} = \frac{1}{R_{r ö d}} + \frac{1}{R_{b l å}} + \frac{1}{R}$

där R_röd är ersättningsresistansen för den röda ovalen och på samma sätt fär R_blå.

Vissa tycker att det hjälper att se ström som ett vattenflöde och resistorer som rör med olika diameter där en stor diameter inte hindrar vattenflödet lika mycket som en liten diameter. Alltså ett sugrör har högre motstånd (resistans) än ett rör med 1 dm i diameter.

Om t.ex. $R_{1} = 10 Ω o c h R_{2} = 10 000 Ω$ här:

Så blir sugröret helt "dominerande". Det är motståndet på 10 000 ohm (sugröret) som nästan helt bestämmer strömmen. Om det däremot ser ut så här:

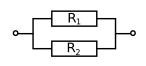
Så är röret med den stora diametern 10 ohm det dominerande. Sätt in värdena i respektive ekvation (serie/parallell ekvationerna) så ser du. Här kommer nästan allt vatten (ström) att gå genom det stora röret, 10 ohm.

Peter skrev:
Va kul att det löste sig!

vilken resistor som bidrar mest till ersättningsresistansen

Det är ekvationerna för seriekoppling och parallellkoppling som avgör vad som bidrar mest. Allt beror på hur de är kopplade. När du ska beräkna ersättningsresistansen i en krets som i labben så är det säkrast att ta ett steg i taget. Om man har något som ser ut så här:

så börjar man med att beräkna ersättningsresistansen för ovalen med formeln för parallellkoppling. Då får man:

där R uppfyller $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ . Sen har man en enkel seriekoppling och det är bara att addera resistanserna. Om man har något mer komplicerat:

så beräknar man först ersättningsresistanserna för ovalerna och sen har man en parallellkoppling med 3 resistorer. Den totala resistansen kan man då räkna ut med

$\frac{1}{R_{t o t}} = \frac{1}{R_{r ö d}} + \frac{1}{R_{b l å}} + \frac{1}{R}$

där R_röd är ersättningsresistansen för den röda ovalen och på samma sätt fär R_blå.

Vissa tycker att det hjälper att se ström som ett vattenflöde och resistorer som rör med olika diameter där en stor diameter inte hindrar vattenflödet lika mycket som en liten diameter. Alltså ett sugrör har högre motstånd (resistans) än ett rör med 1 dm i diameter.

Om t.ex. $R_{1} = 10 Ω o c h R_{2} = 10 000 Ω$ här:

Så blir sugröret helt "dominerande". Det är motståndet på 10 000 ohm (sugröret) som nästan helt bestämmer strömmen. Om det däremot ser ut så här:

Så är röret med den stora diametern 10 ohm det dominerande. Sätt in värdena i respektive ekvation (serie/parallell ekvationerna) så ser du. Här kommer nästan allt vatten (ström) att gå genom det stora röret, 10 ohm.

Tack så mycket för din oerhört bra förklarande kommentar Peter! Nu förstår jag. Väldigt intressant att det kan bli på det sättet.

Svara

Visa senaste svar