Fysmatte PDE uppgift
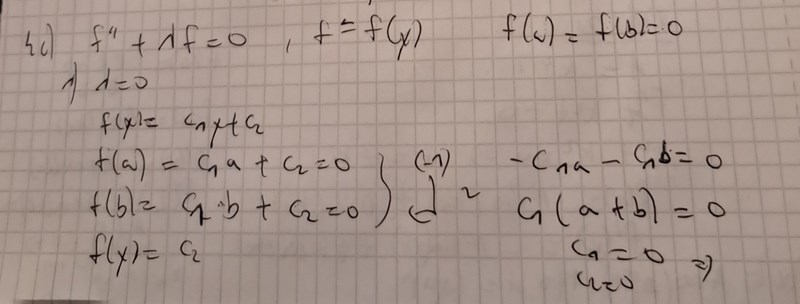


Hej!
I uppgift 4c så har jag kommit fram till denna lösning på fn(y) medan facit har endast tagit med sinus termen och förskjuter y med y-a. Jag förstår ej varför de gjorde det?
Jag är ringrostig över hur du räknar ut det, så jag går på kontroll på slutet.
Om din lösning skall stämma måste f(a) = 0.
Om du sätter in att y= a i f_n(y) så kommer du få A*cos(n*pi *a/(b-a))+B*sin(n*pi*a/(b-a)), och jag trodde målet du ville få till var att då y var a så skulle det som står innanför sinus och cosinus bli ett helt antal pi, och jag ser ingen garanti av att så skulle bli fallet här.
På samma sätt, om y= b får du A*cos(n*pi *b/(b-a))+B*sin(n*pi*b/(b-a)) vilket inte heller ett helt antal pi. Om du däremot antar att
f_n(y) = A*cos(n*pi *(y-a)/(b-a))+B*sin(n*pi*(y-a)/(b-a))
kommer y= a ge (y-a)/(b-a)= 0 och y= b ge (y-a)/(b-a) = 1, så du får då ett helt antal pi:n.
Om du gör den justeringen och sedan sätter in att f(a) skall vara 0 så tror jag du får att A måste vara 0, om vi antar att du inte fick fel på (b)-uppgiften som saknade ett villkor på värdet i första punkten.
Bedinsis skrev:Jag är ringrostig över hur du räknar ut det, så jag går på kontroll på slutet.
Om din lösning skall stämma måste f(a) = 0.
Om du sätter in att y= a i f_n(y) så kommer du få A*cos(n*pi *a/(b-a))+B*sin(n*pi*a/(b-a)), och jag trodde målet du ville få till var att då y var a så skulle det som står innanför sinus och cosinus bli ett helt antal pi, och jag ser ingen garanti av att så skulle bli fallet här.
På samma sätt, om y= b får du A*cos(n*pi *b/(b-a))+B*sin(n*pi*b/(b-a)) vilket inte heller ett helt antal pi. Om du däremot antar att
f_n(y) = A*cos(n*pi *(y-a)/(b-a))+B*sin(n*pi*(y-a)/(b-a))
kommer y= a ge (y-a)/(b-a)= 0 och y= b ge (y-a)/(b-a) = 1, så du får då ett helt antal pi:n.
Om du gör den justeringen och sedan sätter in att f(a) skall vara 0 så tror jag du får att A måste vara 0, om vi antar att du inte fick fel på (b)-uppgiften som saknade ett villkor på värdet i första punkten.
Du menar att jag skriver såhär? Facit svarade enbart fn(y)= sin((npi/b-a)*(y-a)) och tog inte med cosdelen.
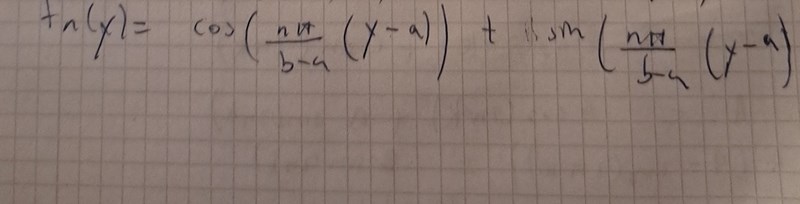
Varför suddade du ut A och B?
Låt oss anta att det fortfarande stod A och B.
Det borde vara lösningen, innan man kontrollerat vad som händer då man sätter in y= a och y= b.
Pröva att sätta in det. Vad blir f_n(a) respektive f_n(b)? Vad kan du säga om A och B för att f_n(a) och f_n(b) båda skall bli 0, som uppgiften angav?
Bedinsis skrev:Varför suddade du ut A och B?
Låt oss anta att det fortfarande stod A och B.
Det borde vara lösningen, innan man kontrollerat vad som händer då man sätter in y= a och y= b.
Pröva att sätta in det. Vad blir f_n(a) respektive f_n(b)? Vad kan du säga om A och B för att f_n(a) och f_n(b) båda skall bli 0, som uppgiften angav?
Facit har inte med A och B i alla fall. Men om fn(a)=0 så är det då A=0. För y=b har vi fn(b)=Bsin(npi) => B=0. Om vi ska ha icke trivial lösning så måste A och B vara skilda från 0.
destiny99 skrev:För y=b har vi fn(b)=Bsin(npi) => B=0.
Jaså? Vad är sinus av pi?
Bedinsis skrev:destiny99 skrev:För y=b har vi fn(b)=Bsin(npi) => B=0.
Jaså? Vad är sinus av pi?
Man kan tänka att antingen B =0 eller sin(npi)=0. För sin(npi)=0=> npi=npi=>1=1
destiny99 skrev:Bedinsis skrev:destiny99 skrev:För y=b har vi fn(b)=Bsin(npi) => B=0.
Jaså? Vad är sinus av pi?
Man kan tänka att antingen B =0 eller sin(npi)=0. För sin(npi)=0=> npi=npi=>1=1
Så med andra ord behöver inte B vara 0.
Jag undrar dock varför facit hävdar att B måste vara 1, om det är som du skrev i inlägg #3.
Bedinsis skrev:destiny99 skrev:Bedinsis skrev:destiny99 skrev:För y=b har vi fn(b)=Bsin(npi) => B=0.
Jaså? Vad är sinus av pi?
Man kan tänka att antingen B =0 eller sin(npi)=0. För sin(npi)=0=> npi=npi=>1=1
Så med andra ord behöver inte B vara 0.
Jag undrar dock varför facit hävdar att B måste vara 1, om det är som du skrev i inlägg #3.
Jag vet inte. Men tror det har att göra med att de vill ha icke trivial lösning för B skild från 0 och då sätter de bara den till 1.

