g(x), g'(x) och g''(x)
Hej,
Jag är lite osäker här och behöver lite vägledning.
fråga 1 : Bestäm med hjälp av grafen de värden på x för vilka det gäller att g'(x) ≥ 0 och g(x) ≤ 0 (båda villkoren skall vara uppfyllda).
så här tänkte jag:
g'(x) ≥ 0 -----> -7,5 ≤ x ≤ 10
g(x) ≤ 0 ------> 2 ≤ x ≤ 18
då är värden som uppfyller villkoren 2 ≤ x ≤ 10
fråga 2 : För vilket eller vilka värden på x är g''(x) ≥ 0
Jag skrev att x >10
Är jag på rätt spår?
Tack på förhand !
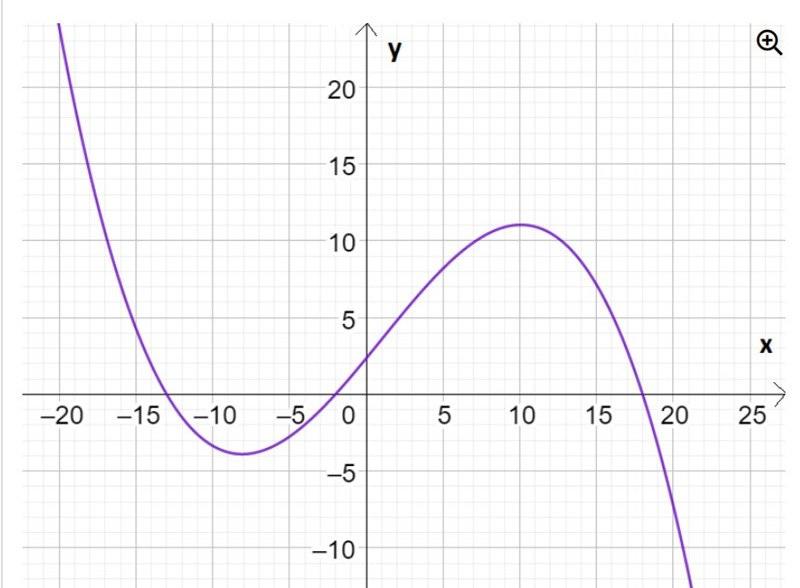
Visar grafen g(x)? Jag håller inte med om att g(x) < 0 i intervallet 2 < x < 18.
Förlåt! jag skrev fel i första frågan. Nu har jag justerat den.
När det gäller grafen så visar den en tredjegradsfunktionen g(x).
är den rätt nu? g(x) ≤ 0 ------> 2 ≤ x ≤ 18
Vad är g(2)?
g(2) = 5, antar jag
Är 5 < 0?
Absolut inte. Då blir g(x) ≤ 0 ------> x >18. Eller?
T.ex., men den är väl < 0 på andra ställen också?
Just det! mellan -13 och -2
då g(x) ≤ 0 -------> x > 18 samt -13 < x < -2
När det gäller g'(x) och g''(x) skrev jag så här:
g'(x) ≥ 0 -----> -7,5 ≤ x ≤ 10
g''(x) ≥ 0 -------> x >10
Stämmer det?
Vad är ditt svar på fråga 1?
Jag skulle säga: -7,5 < x < -2. Stämmer det?
Ja.
Fråga 2: Om g''(x) > 0 så ökar derivatan.
Tack för hjälpen ! Nu förstår jag.


