Gammalt nationellt.

Corokia cotoneaster skrev:

Hej!

Jag förstår inte riktigt följande fråga:

För vilka vinklar i intervallet $0° <v<90°$ gäller att $\sin 3v<\frac{1}{2}$?

Jag förstår helt enkelt inte vad jag bör göra:(

Börja med att lösa olikheten sin(3v) < 1/2.

Välj sedan de vinklar ur lösningen som uppfyller villkoret 0° < v < 90°

Yngve skrev:

Corokia cotoneaster skrev:

Hej!

Jag förstår inte riktigt följande fråga:

För vilka vinklar i intervallet $0° <v<90°$ gäller att $\sin 3v<\frac{1}{2}$?

Jag förstår helt enkelt inte vad jag bör göra:(

Börja med att lösa olikheten sin(3v) < 1/2.

Välj sedan de vinklar ur lösningen som uppfyller villkoret 0° < v < 90°

 Det står stilla för mig.. Hur börjar jag?

$$\begin{gathered} \sin 3v<\frac{1}{2} \\ 3v<{\sin }^{-1}\left(\frac{1}{2}\right) \end{gathered}$$

Jag skulle börja med att lösa ekvationen* $\sin(v)=\frac{1}{2}$. Sedan skulle jag rita upp enhetscirkeln och markera in värdena på $v$.

*Jag tycker bättre om att lösa ekvationer än olikheter, för då blir det mindre rörigt i huvudet på mig.

$$\begin{gathered} 3v=150° + n *360° \\ v= 50 + n * 120° \\ Eller \\ 3v= 30° + n * 360° \\ v = 10° + n * 120° \end{gathered}$$

Edit : slarvfel

Corokia cotoneaster skrev:

$$\begin{gathered} 3v=150° + n *360° \\ v= 50 + n * 360° \\ Eller \\ 3v= 30° + n * 360° \\ v = 10° + n * 360° \end{gathered}$$

 Rätt tänkt men du missade en detalj.

Du måste dividera hela HL med 3 så du får

v = 50° + n*120°

v = 10° + n*120°

Yngve skrev:

Corokia cotoneaster skrev:

$$\begin{gathered} 3v=150° + n *360° \\ v= 50 + n * 360° \\ Eller \\ 3v= 30° + n * 360° \\ v = 10° + n * 360° \end{gathered}$$

 Rätt tänkt men du missade en detalj.

Du måste dividera hela HL med 3 så du får

v = 50° + n*120°

v = 10° + n*120°

 Jag märkte och ändrade det felet :)

Du har missat att även $360^\circ$ skall delas med 3 (inte för att det spelar någon roll i det här fallet, men...).

Härefter skulle jag markera vinklarna $0^\circ$, $10^\circ$, $50^\circ$ och $90^\circ$ i enhetscirkeln, och fundera på i vilka av de olika intervallen $\sin(3v)$ är större respektive mindre än ½.

Smaragdalena skrev:

Du har missat att även $360^\circ$ skall delas med 3 (inte för att det spelar någon roll i det här fallet, men...).

Härefter skulle jag markera vinklarna $0^\circ$, $10^\circ$, $50^\circ$ och $90^\circ$ i enhetscirkeln, och fundera på i vilka av de olika intervallen $\sin(3v)$ är större respektive mindre än ½.

 Jag ändrade mitt fel som jag gjorde.

Menar du såhär:

$$\begin{gathered} 0°<v<10° \\ 50°<90° \end{gathered}$$

Corokia cotoneaster skrev:

 Jag ändrade mitt fel som jag gjorde.

Menar du såhär:

$$\begin{gathered} 0°<v<10° \\ 50°<90° \end{gathered}$$

Om du menar 0° < v < 10° och 50° < v < 90° så är det rätt.

Ja precis :)

Jag skulle lösa sista steget på följande sätt:

Enhetscirkeln ger att sin(3v) < 1/2 då

-210° + n*360 < 3v < 30° + n*360°

-70° + n*120° < v < 10° + n*120°

Vi letar efter de v som uppfyller 0° < v < 90°

För n = 0 får vi då 0° < v < 10°

För n = 1 får vi då 50° < v < 90°

Yngve skrev:

Enhetscirkeln ger att sin(3v) < 1/2 då

-210° + n*360 < 3v < 30° + n*360°

-70° + n*120° < v < 10° + n*120°

Vi letar efter de v som uppfyller 0° < v < 90°

För n = 0 får vi då 0° < v < 10°

För n = 1 får vi då 50° < v < 90°

 Ska fundera en stund på det där, förstår inte riktigt vad du menar med enhetscirkeln..

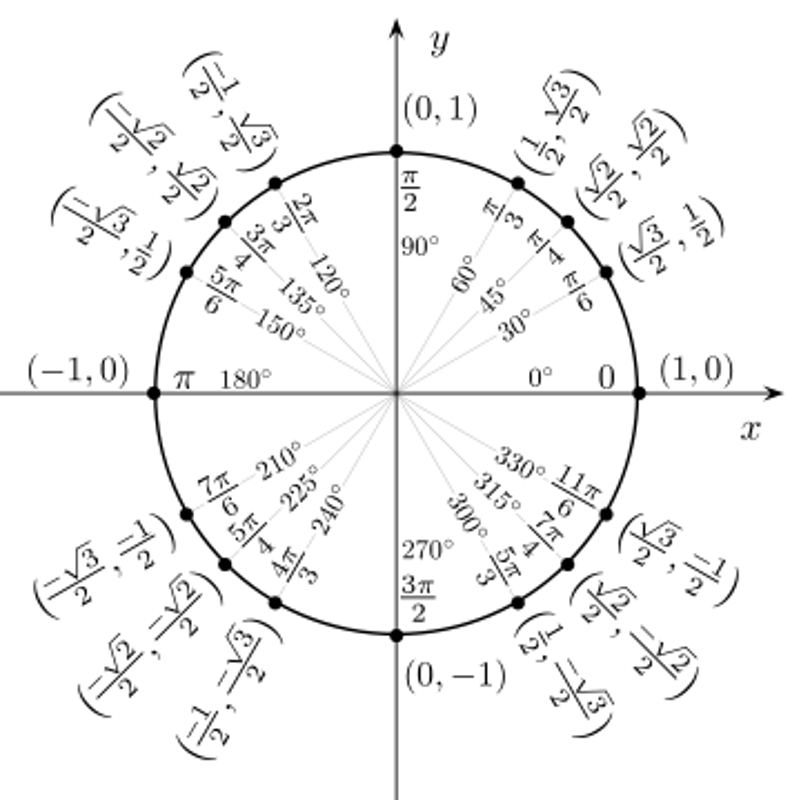
Enhetscirkeln är din bästa vän, när det gäller att lösa trigonometriska ekvationer.