Gauss.
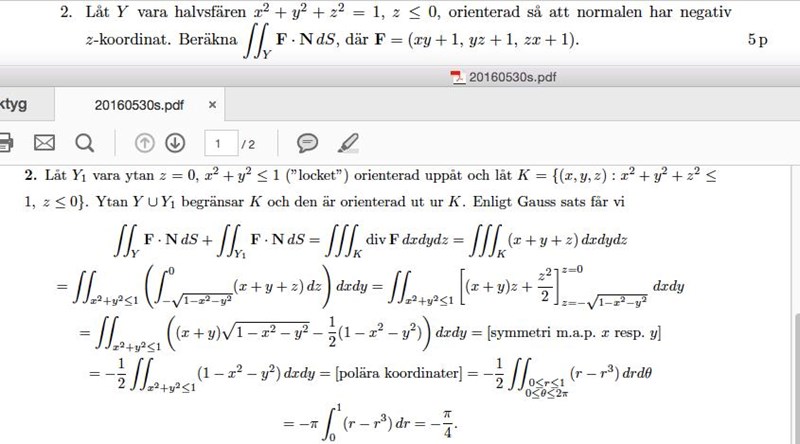
Har en fråga ang den här, sätter man nedre gräns till -sqrtlala. pga att vi har ett 'lock'?
Jag förstår inte varför du tänker dig att det är "locket". Tänk dig ett enklare fall, nämligen . Här kan vi beskriva en cirkel genom . Vi vill nu lösa ut och får då . Kan du säga mig vilken del av cirkeln som beskrivs av den negativa respektive positiva delen av i detta fall?
Ser du likheten med sfären i ?
Om AlvinB vore här kunde han säkert fixa sina fina illustrationer som är mycket bättre än min vaga förklaring, men man gör väl sitt bästa/ett försök i alla fall :)
Nej, locket är den övre gränsen där z=0.
Nyckeln till varför -gränserna ser ut som de gör är att området har villkoret . Detta gör att vi får en halvsfär som ligger under -planet:

Att man får gränserna och beror alltså på att vårt område går från ytan upp till (-planet).
Notera skillnaden om vi istället haft villkoret . Då hade området sett ut så här:

och då hade gränserna istället blivit till .
AlvinB skrev:Nyckeln till varför -gränserna ser ut som de gör är att området har villkoret . Detta gör att vi får en halvsfär som ligger under -planet:
Att man får gränserna och beror alltså på att vårt område går från ytan upp till (-planet).
Notera skillnaden om vi istället haft villkoret . Då hade området sett ut så här:
och då hade gränserna istället blivit till .
Tack för en excellent förklaring <3



