Gauss divergenssats


Vi börjar med 1b :-)
Jag försöker beräkna den här integralen på mitt sätt. (Och jag har väl typ fått för mig att alltid lättast att integrera m.a.p först, för att få bort den och bara ha kvar för att sen gå över till polära, vet inte.. )
Iallfall.. så det jag hade velat gjort är att gränser är så alltså beräkna
Men det ser ut att vara rätt meckigt. ? Eller tänker jag fel?
Din metod är faktiskt rätt bra i detta fall om vi korrigerar några saker. Det första är att du slarvar lite med gränserna. Det är ju så att kroppen går från ytan upp till planet . Det ger gränserna:
(Om du har svårt att förstå detta, rita upp alltsammans i Geogebra)
Det blir även lite svårt om man använder vanliga polära koordinater. Det är klokare att använda elliptiska koordinater motsvarande ellipsen vi har. Om man räknar igenom det får man:
Härifrån skulle vi vilja ha ett variabelbyte och sådant att
och
eftersom vi då skulle kunna använda oss av trigonometriska ettan. Vi räknar då fram att och . Variabelbytet blir alltså:
(Detta är samma variabelbyte som användes för ytintegralen)
Jacobideterminanten blir då:
således är . I och med att variabelbytet i vårt fall representerar området (ellipsen) blir gränserna och . Då blir integralen:
AlvinB skrev:Din metod är faktiskt rätt bra i detta fall om vi korrigerar några saker. Det första är att du slarvar lite med gränserna. Det är ju så att kroppen går från ytan upp till planet . Det ger gränserna:
(Om du har svårt att förstå detta, rita upp alltsammans i Geogebra)
Det blir även lite svårt om man använder vanliga polära koordinater. Det är klokare att använda elliptiska koordinater motsvarande ellipsen vi har. Om man räknar igenom det får man:
Härifrån skulle vi vilja ha ett variabelbyte och sådant att
och
eftersom vi då skulle kunna använda oss av trigonometriska ettan. Vi räknar då fram att och . Variabelbytet blir alltså:
(Detta är samma variabelbyte som användes för ytintegralen)
Jacobideterminanten blir då:
således är . I och med att variabelbytet i vårt fall representerar området (ellipsen) blir gränserna och . Då blir integralen:
Men vilken svår fråga det här var.. :S
Jag ska kolla på hur du gjorde för att lösa den. Men har en fråga innan.
Om detta hade istället varit en cylinder då hade väl eller hur? men eftersom detta är en kon, så kan z inte vara inne i [0,1]? Jag tänker på den här uppgiften tex:
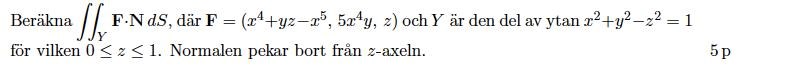
Se de gulmarkerade

Jag har svårt att tro att den där frågan och det där svaret hör ihop. I svaret verkar det som att ytan är en cylinder, men i uppgiften talas det om en hyperboloid.
Är du säker på att uppgiften och frågan hänger ihop?
EDIT: Ser nu att divergensen för fältet inte stämmer heller, vilket tyder på att det är facit till en annan uppgift.
AlvinB skrev:Jag har svårt att tro att den där frågan och det där svaret hör ihop. I svaret verkar det som att ytan är en cylinder, men i uppgiften talas det om en hyperboloid.
Är du säker på att uppgiften och frågan hänger ihop?
EDIT: Ser nu att divergensen för fältet inte stämmer heller, vilket tyder på att det är facit till en annan uppgift.
Oj skickade fel uppg (skämdumparna på mac heter alltid densamma, suck)
Här är det korrekta
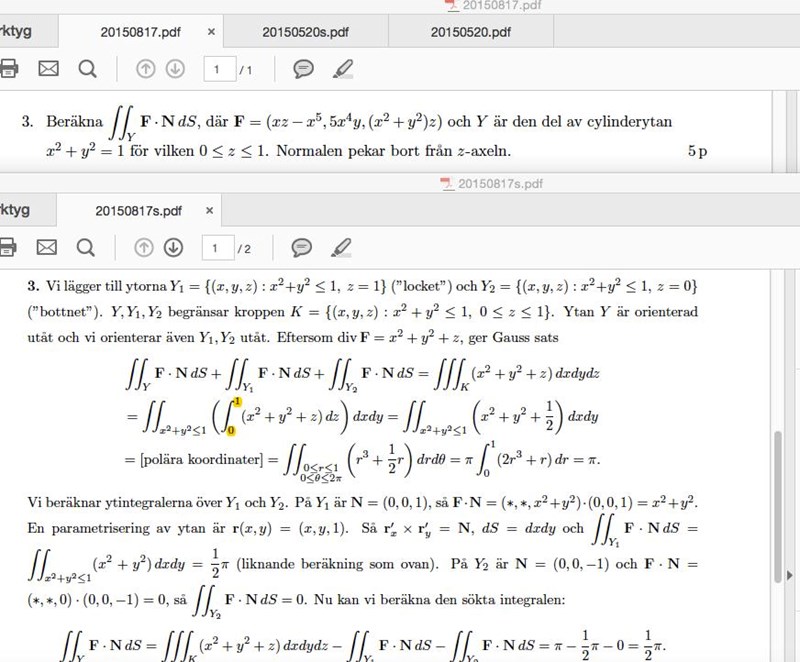
Ja, att innebär att kroppens tvärsnittsyta är lika stor rakt igenom den. En kon är inte en sådan kropp, alltså får vi krångligare integrationsgränser.
AlvinB skrev:Ja, att innebär att kroppens tvärsnittsyta är lika stor rakt igenom den. En kon är inte en sådan kropp, alltså får vi krångligare integrationsgränser.
Då är det mkt klarare :) tack så mkt!! :D


