Gauss sats, jämföra formeln.

Hej!

• Nej du har rätt, det stämmer att $\frac{-\pi}{3}\neq\frac{2\pi}{3}$, men som tur är så är det inte relevant för den här uppgiften. Det du ska lägga märke till är att summan av flödet (ytintegralerna) är $\frac{-\pi}{3}+\pi=\frac{2\pi}{3}$, dvs. samma som beräkningen av trippelintegralen med hjälp av Gauss sats.
• Vad menar du? I beräkningen av ytintegralen för ytan $Y_{2}$ så behöver du bara använda att du får dubbelintegralen med integrand $1$ över en cirkel med radie $1$. Du vet att $\displaystyle \text{Area}\left(Y_{2}\right)=\iint_{Y_{2}}dA=\pi\cdot 1^2=\pi$.

Moffen skrev:

Hej!

• Nej du har rätt, det stämmer att $\frac{-\pi}{3}\neq\frac{2\pi}{3}$, men som tur är så är det inte relevant för den här uppgiften. Det du ska lägga märke till är att summan av flödet (ytintegralerna) är $\frac{-\pi}{3}+\pi=\frac{2\pi}{3}$, dvs. samma som beräkningen av trippelintegralen med hjälp av Gauss sats.
• Vad menar du? I beräkningen av ytintegralen för ytan $Y_{2}$ så behöver du bara använda att du får dubbelintegralen med integrand $1$ över en cirkel med radie $1$. Du vet att $\displaystyle \text{Area}\left(Y_{2}\right)=\iint_{Y_{2}}dA=\pi\cdot 1^2=\pi$.

hej!

• ok
• men det står ju att $z=1$ ,varför tar dom i integralens beräkning att det är $[0, \sqrt{z}]$?

Pratar vi om samma problem längre? Allt jag kan se i beräkningen av $\displaystyle\iint_{Y_{2}}\vec{F}\cdot\vec{N}ds$ är:

Vart kommer $\sqrt{z}$ in i bilden?

Roten av z dyker upp när de använder Gauss sats. Man integrerar över volymen K som begränsas av Y1 och Y2. Den kropp är innanför Y1, och sedan kommer ett lock Y2. Om du tittar på beskrivningen av Y1 ser du att det står z=x^2+y^2 vilket översatt i cylindriska koordinater blir z=r^2. Om du då ska integrera över volymen som omsluts av Y1 och Y2 kommer då 0<=r<=sqrt(z). Så integrationsgränsen för r blir då 0 och sqrt(z)

Hondel skrev:

Roten av z dyker upp när de använder Gauss sats. Man integrerar över volymen K som begränsas av Y1 och Y2. Den kropp är innanför Y1, och sedan kommer ett lock Y2. Om du tittar på beskrivningen av Y1 ser du att det står z=x^2+y^2 vilket översatt i cylindriska koordinater blir z=r^2. Om du då ska integrera över volymen som omsluts av Y1 och Y2 kommer då 0<=r<=sqrt(z). Så integrationsgränsen för r blir då 0 och sqrt(z)

okej tack

men när de beräknar ut integralen $\iint_{dK} F \cdot N dS$ så skriver dom i facit att de paramatiserar $Y_1$ som $(x,y,z=x^2+y^2)$ (antar att de låter $x,y$ variera fritt här?  men hur har dom fått ut normalvektorn $N=(2x,2y,-1)$. ? 

Jag känner till $r'_x \times r'_y$ som i Stokes sats, är det, det dom använder här också då? svar, ja. 

Varför kan man inte bra ta en norma a la $N=(0,0,-1)$ eller $N=(0,0,1)$ ?  Som disskuteras i min andra tråd: HÄR

i det här fallet skulle vi ha en positiv normal, eftersom vi har ett lock?

sannakarlsson1337 skrev:

...

men när de beräknar ut integralen $\iint_{dK} F \cdot N dS$ så skriver dom i facit att de paramatiserar $Y_1$ som $(x,y,z=x^2+y^2)$ (antar att de låter $x,y$ variera fritt här?  men hur har dom fått ut normalvektorn $N=(2x,2y,-1)$. ? 

(x'(z),y'(z),-1) eftersom normalvektorn skall vara riktad neråt

Smaragdalena skrev:

sannakarlsson1337 skrev:

Visa föregående citat

...

men när de beräknar ut integralen $\iint_{dK} F \cdot N dS$ så skriver dom i facit att de paramatiserar $Y_1$ som $(x,y,z=x^2+y^2)$ (antar att de låter $x,y$ variera fritt här?  men hur har dom fått ut normalvektorn $N=(2x,2y,-1)$. ? 

(x'(z),y'(z),-1) eftersom normalvektorn skall vara riktad neråt

Men det är ju ett lock? 

Jag blandade nog ihop några av dina trådar.

Hej!

men hur har dom fått ut normalvektorn $N=\left(2x,2y,-1\right)$. ?

Inte allt för ingående eller med alla detaljer, men du kan tänka på följande vis:

Låt $f\left(x,y\right)$ vara en lämplig funktion definierad på ett lämpligt område $\Omega\subset\mathbb{R}^{2}$.

Grafen till denna funktion ges då av mängden punkter $\left(x,y,z\right)$ sådana att $z=f\left(x,y\right)$ inom det givna området. Givet $\sigma\left(x,y,z\right)=\left(x,y,f\left(x,y\right)\right)$, så får vi en yta $S$, $\sigma: \Omega\to S$ (grafen till funktionen $f$).

I varje punkt kan vi lokalt definiera ett tangentplan. Vi får lätt en bas för detta tangentplan $T_{p}S$ som $T_{p}S=\text{span}\{\sigma_{x},\sigma_{y}\}$. En normal till tangentplanet i en punkt ger då även en normal till ytan i samma punkt.

Eftersom vi har en bas för tangentplanet så kan vi hitta en normal genom att kryssa våra basvektorer, eller hur?

Vi får då att en normal till ytan i en punkt kan beräknas som $\sigma_{x}\times \sigma_{y}=...=\left(f_{x},f_{y},-1\right)$.

Så med ditt $z=x^2+y^2$ har vi $f\left(x,y\right)=x^2+y^2$, vilket ger $f_{x}=2x$ och  $f_{y}=2y$.

Moffen skrev:

Hej!

men hur har dom fått ut normalvektorn $N=\left(2x,2y,-1\right)$. ?

Inte allt för ingående eller med alla detaljer, men du kan tänka på följande vis:

Låt $f\left(x,y\right)$ vara en lämplig funktion definierad på ett lämpligt område $\Omega\subset\mathbb{R}^{2}$.

Grafen till denna funktion ges då av mängden punkter $\left(x,y,z\right)$ sådana att $z=f\left(x,y\right)$ inom det givna området. Givet $\sigma\left(x,y,z\right)=\left(x,y,f\left(x,y\right)\right)$, så får vi en yta $S$, $\sigma: \Omega\to S$ (grafen till funktionen $f$).

I varje punkt kan vi lokalt definiera ett tangentplan. Vi får lätt en bas för detta tangentplan $T_{p}S$ som $T_{p}S=\text{span}\{\sigma_{x},\sigma_{y}\}$. En normal till tangentplanet i en punkt ger då även en normal till ytan i samma punkt.

Eftersom vi har en bas för tangentplanet så kan vi hitta en normal genom att kryssa våra basvektorer, eller hur?

Vi får då att en normal till ytan i en punkt kan beräknas som $\sigma_{x}\times \sigma_{y}=...=\left(f_{x},f_{y},-1\right)$.

Så med ditt $z=x^2+y^2$ har vi $f\left(x,y\right)=x^2+y^2$, vilket ger $f_{x}=2x$ och  $f_{y}=2y$.

Kryssprodukten är jag med på, men är inte med på just minus ettan där. 

Kryssprodukten är jag med på, men är inte med på just minus ettan där. 

Det går inte ihop, minus ettan kommer från kryssprodukten.

Har du beräknat den?

Vad är $\sigma_{x}$?

Vad är $\sigma_{y}$?

Vad är $\sigma_{x}\times\sigma_{y}$?

Moffen skrev:

Kryssprodukten är jag med på, men är inte med på just minus ettan där. 

Det går inte ihop, minus ettan kommer från kryssprodukten.

Har du beräknat den?

Vad är $\sigma_{x}$?

Vad är $\sigma_{y}$?

Vad är $\sigma_{x}\times\sigma_{y}$?

yes, det gjorde jag. men i tidigare uppgifter så "har dom inte" räknat ut kryssprodukten, utan bara utgått från att

• är det ett lock, så är N=+(0,0,1)
• är det ett botten, så är det N=-(0,0,1)

så liksom, varför beräkna kryssprodukten i det här fallet?  kolla den här uppg: 

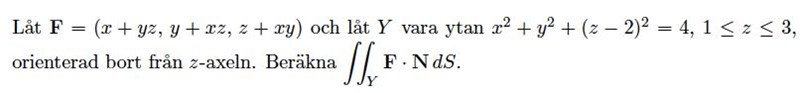
där tar dom ingen kryssprodukt ? =)

Varför skulle de göra det, när man kan se det bara man ritar upp det? Det är ett lock som är ett plant område (x och y kan vara olika, z är konstant) och eftersom det är ett lock är riktningen bortåt samma sak som riktningen uppåt. Det är en botten som är ett plant område (x och y kan vara olika, z är konstant) och eftersom det är en botten så är riktningen bortåt samma sak som riktningen neråt.