Gauss sats, rymdpolära or not.
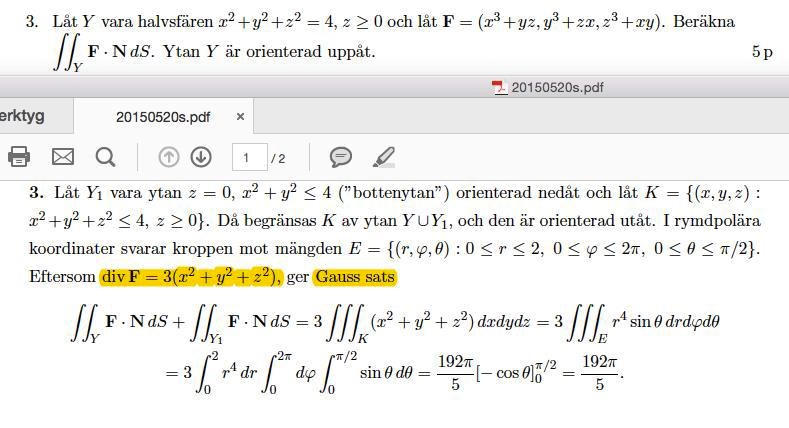
Varför måste man gå över till rymdpolära koordinater för denna? jag satt och beräknade att
varför kan man inte räkna så?
Om du lyckades få fram rätt svar, så kan man räkna så. Den som har skrivit facit tyckte det var lättare att göra på det andra sättet.
Smaragdalena skrev:Om du lyckades få fram rätt svar, så kan man räkna så. Den som har skrivit facit tyckte det var lättare att göra på det andra sättet.
Jaha okej, så det är rätt och göra så. DÅ har jag räknat fel någonstans. Är inte så bekväm med sfäriska (..yet hehe)
Då är det en bra anledning att räkna med dem.
Det finns nästan alltid mer än ett sätt att lösa en viss uppgift i matematik. När jag pluggade matte för många år sedan, satt jag i flera timmar och försökte lösa en uppgift - jag var tvungen att själv fundera ut hur jag skulle flytta och rotera en kropp i ett koordinatsystem för att kunna beräkna svaret. Jag slet en evighet, och fick till slut fram rätt svar. Min kompis hade läst en sida längre i läroboken. Hon skrev en lösning på två rader. Jag tror trots allt att jag lärde mig mer!
Smaragdalena skrev:Då är det en bra anledning att räkna med dem.
Det finns nästan alltid mer än ett sätt att lösa en viss uppgift i matematik. När jag pluggade matte för många år sedan, satt jag i flera timmar och försökte lösa en uppgift - jag var tvungen att själv fundera ut hur jag skulle flytta och rotera en kropp i ett koordinatsystem för att kunna beräkna svaret. Jag slet en evighet, och fick till slut fram rätt svar. Min kompis hade läst en sida längre i läroboken. Hon skrev en lösning på två rader. Jag tror trots allt att jag lärde mig mer!
Hmmm.. jag förstår.
Det känns som att man måste ha mer koll på sfäriska koordinater, än att göra så som jag gjorde. Nackdelen/risken är ju att man dock räknar fel någonstans på vägen. Än att bara direkt slänga in sfäriska koordinater utan att ha koll på hur kroppen blir då med det bytet.
Man behöver ha koll på sfäriska koordinater, så är det bara. Träna, träna, träna (trist).
Smaragdalena skrev:Man behöver ha koll på sfäriska koordinater, så är det bara. Träna, träna, träna (trist).
Aaa nu försöker jag se ett mönster, ett slags "okej, det här kommer bli jättekonstigt, mkt krångliga uträkningar osv osv" och börjar fatta lite mer nu. Men jag kommer fortf till denna uppg. Jag gör så här:
och gör polära koordinater.
DivF = så vi kommer jobba med tre integraler, (pga. normalen blev lite konstigt och vad jag kan tänka mig - svår räknad: (rätta mig gärna om jag gör fel, eller om jag tänker fel)
Så polära koordinater.
Här tycker jag det blir konstigt..
.
Liksom om jag integrerar detta, subsistutera in dessa gränser. Så får jag ingen relation med varken eller ., så man kan fortsätta räknandet.
Så vad är det som blir konstigt (alltså det ska ju fungera med detta sätt också, istället för sfäriska, men försker bara förstå här, hehe)
Om du har polära koordinater skall du inte ha kvar något z. Du kanske tänker på cylindriska koordinater?
z tillhör intervallet [0 till roten ur 4-z^2] ser väldigt konstigt ut. Är det samma z?
Vad beträffar polärt och z så kan man använda polära för bara x och y, men låta z vara. Det heter cylindriska koordinater. Om det är det du vill använda här vet jag inte.
Smaragdalena skrev:Om du har polära koordinater skall du inte ha kvar något z. Du kanske tänker på cylindriska koordinater?
Aaa menar det.
Laguna skrev:z tillhör intervallet [0 till roten ur 4-z^2] ser väldigt konstigt ut. Är det samma z?
Vad beträffar polärt och z så kan man använda polära för bara x och y, men låta z vara. Det heter cylindriska koordinater. Om det är det du vill använda här vet jag inte.
aha okej, så när jag vill ha kvar z så blir det cylindriska..
Men fortfarande återstår. Hur skall det se ut?
mrlill_ludde skrev:Smaragdalena skrev:Om du har polära koordinater skall du inte ha kvar något z. Du kanske tänker på cylindriska koordinater?
Aaa menar det.
Du menar nog att z ligger i intervallet från 0 till .
Smaragdalena skrev:mrlill_ludde skrev:Smaragdalena skrev:Om du har polära koordinater skall du inte ha kvar något z. Du kanske tänker på cylindriska koordinater?
Aaa menar det.
Du menar nog att z ligger i intervallet från 0 till .
Hmm...
varför blir det intervallet? (& typ inte tex. ?)
för det jag känner till med cylindriska är:
Transformering till kartesiska koordinater sker genom
x=rcosθ
y=rsinθ
z=h
och för volymelementet gäller
dV=rdrdθdh
Standardfråga 1a: Har du ritat?
Om man byter namn på z till h är det h som skall ha det intervallet.
Om R är halvsfärens radie skall variabeln r gå från 0 till R. När r = R är h = 0. När r = 0 är man i toppen av halvklotet. Jag kan ha missar ett rottecken över alltihop, skall kolla det när jag kommer till en dator - jag får dålig överblick på mobilen.
Det skall vara .
Smaragdalena skrev:Det skall vara .
ja jaa! Okej. Jag ska kolla på det här lite närmare. hehe. På återseende =)
Smaragdalena skrev:Det skall vara .
Nu har jag räknat.. Och hur ska jag komma förbi det här nu? tips?
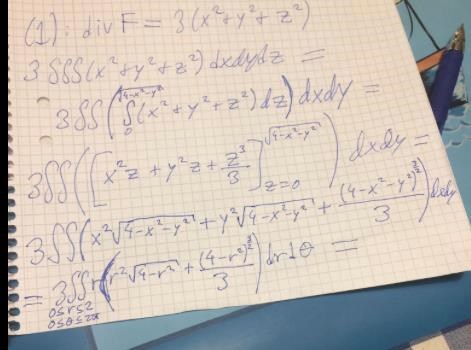
Krånglar jag till det?
För det här finns ju inte heller någon symmetri eller? kan jag kapa å således bara få kvar? och även där 'kapa' också pga symmetri, och få endast ??
Krånglar jag till det?
Ja. Du borde gå över till sfäriska koordinater, precis som man gjort i facit, så skulle du ha fått mycket enklare beräknangar.
Smaragdalena skrev:Krånglar jag till det?
Ja. Du borde gå över till sfäriska koordinater, precis som man gjort i facit, så skulle du ha fått mycket enklare beräknangar.
Okej, nu har jag kollat på det här talet. (tagit lite julledigt)
Då ser jag följande:
 r är ju lätt och se det är ju bara
r är ju lätt och se det är ju bara
när det kommer till fi (tror den heter fi va?) och theta, så tycker jag det blir lite krångligare. Om jag har min funktion
hur ska jag tänka där då?
Den uttalas fi. Jag brukar skriva phi, men fi kanske också går bra.
mrlill_ludde skrev:Smaragdalena skrev:Krånglar jag till det?
Ja. Du borde gå över till sfäriska koordinater, precis som man gjort i facit, så skulle du ha fått mycket enklare beräknangar.
Okej, nu har jag kollat på det här talet. (tagit lite julledigt)
Då ser jag följande:
r är ju lätt och se det är ju bara
när det kommer till fi (tror den heter fi va?) och theta, så tycker jag det blir lite krångligare. Om jag har min funktion
hur ska jag tänka där då?
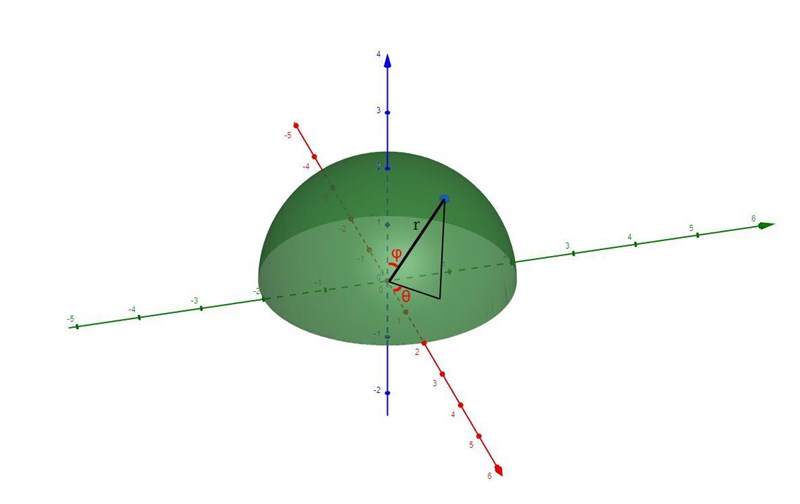
Enligt definitionerna i din bild så är:
- radien. Eftersom vår kropp är en halvsfär med radie kommer denna att variera mellan och .
- vinkeln mellan -axeln och radien (kolatituden). Då vi har en halvsfär kommer denna att variera mellan och
- vinkeln mellan -axeln och radien (longituden). Halvsfären går ju hela varvet runt i -planet, alltså varierar denna mellan och .
Notera att i facit har man valt att kalla kolatituden för och longituden för istället.
AlvinB skrev:mrlill_ludde skrev:Smaragdalena skrev:Krånglar jag till det?
Ja. Du borde gå över till sfäriska koordinater, precis som man gjort i facit, så skulle du ha fått mycket enklare beräknangar.
Okej, nu har jag kollat på det här talet. (tagit lite julledigt)
Då ser jag följande:
r är ju lätt och se det är ju bara
när det kommer till fi (tror den heter fi va?) och theta, så tycker jag det blir lite krångligare. Om jag har min funktion
hur ska jag tänka där då?
Enligt definitionerna i din bild så är:
- radien. Eftersom vår kropp är en halvsfär med radie kommer denna att variera mellan och .
- vinkeln mellan -axeln och radien (kolatituden). Då vi har en halvsfär kommer denna att variera mellan och
- vinkeln mellan -axeln och radien (longituden). Halvsfären går ju hela varvet runt i -planet, alltså varierar denna mellan och .
Notera att i facit har man valt att kalla kolatituden för och longituden för istället.
Jaha okej, men om vi inte hade en halvsfär, utan en hel då hade eller hur? och om man hade en cylinder också typ?
Men om jag ska räkna ut det där vi vet ju att i polära är ju.. Men vet inte vad jag ska göra med (försöker att inte bara memorera facit)
och vad blir
Nej, hade vi haft en hel sfär hade eftersom radien skall variera mellan att peka uppåt () och att peka nedåt ().
Om vi istället hade haft en cylinder hade det varit svårt att använda sfäriska koordinater. Då är det istället lämpligare att använda cylindriska koordinater.
I planpolära koordinater är som du säger . Motsvarande samband i sfäriska koordinater är .
Volymelementet i sfäriska koordinater är lika med . Detta kan härledas med Jacobideterminanten.
AlvinB skrev:Nej, hade vi haft en hel sfär hade eftersom radien skall variera mellan att peka uppåt () och att peka nedåt ().
Om vi istället hade haft en cylinder hade det varit svårt att använda sfäriska koordinater. Då är det istället lämpligare att använda cylindriska koordinater.
I planpolära koordinater är som du säger . Motsvarande samband i sfäriska koordinater är .
Volymelementet i sfäriska koordinater är lika med . Detta kan härledas med Jacobideterminanten.
och då? alltså får vi som dom säger i lösningen? (vill bara vara helt hundra)
Nej,
gäller enbart i planpolära koordinater (det tvådimensionella koordinatsystemet). I sfäriska koordinater (det tredimensionella koordinatsystemet) finns ett annat samband, nämligen .
När vi då går över från kartesiska till byter vi ut mot . När detta multipliceras ihop med differentialen får vi integralen:
AlvinB skrev:Nej,
gäller enbart i planpolära koordinater (det tvådimensionella koordinatsystemet). I sfäriska koordinater (det tredimensionella koordinatsystemet) finns ett annat samband, nämligen .
När vi då går över från kartesiska till byter vi ut mot . När detta multipliceras ihop med differentialen får vi integralen:
jaha okej så $$dxdydz = r^2\sin(\varphi)\ drd\theta d\varph$$
Fast om du håller konstant, så gäller det att , där . Varje snitt vinkelrätt mot -axeln är en cirkel.
Smaragdalena skrev:Fast om du håller konstant, så gäller det att , där . Varje snitt vinkelrätt mot -axeln är en cirkel.
När väljer man att hålla z konstant? 😳
Det var bara ett försök att få dig att förstå hur klotet ser ut och hur det hänger ihop med de kartesiska och de polära koordinaterna.
AlvinB skrev:Nej,
gäller enbart i planpolära koordinater (det tvådimensionella koordinatsystemet). I sfäriska koordinater (det tredimensionella koordinatsystemet) finns ett annat samband, nämligen .
När vi då går över från kartesiska till byter vi ut mot . När detta multipliceras ihop med differentialen får vi integralen:
Men det är en sak som jag må missuppfattar, för
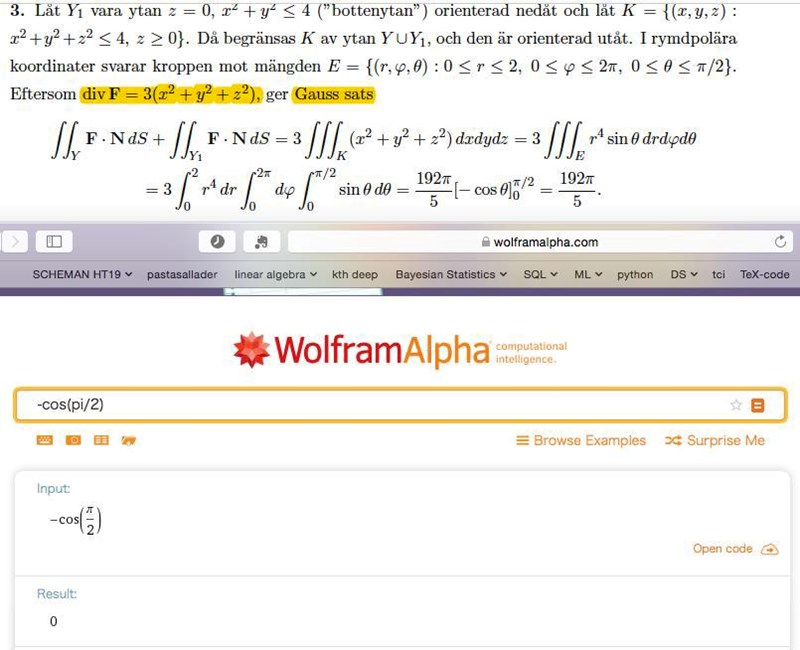
alltså, detta ska ju mulitpliceras, något multiplicerat med 0 är ju 0.. Så hänger inte med...
För jag räknade såhär? (jag vet jag har räknat fel på r. men struntsamma)
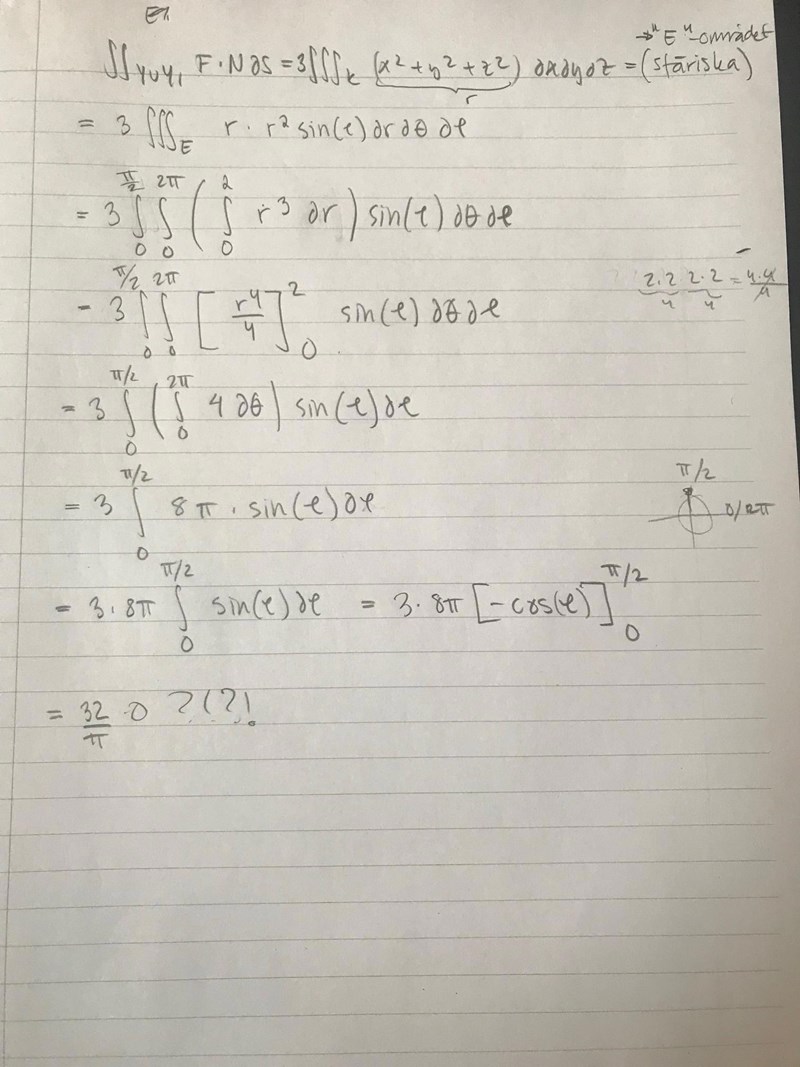
Visserligen är , men !
Dessutom har du missat att och inte . (EDIT: Såg nu att du insett det själv)

Hur kunde bli ?
AlvinB skrev:Visserligen är , men !
Dessutom har du missat att och inte . (EDIT: Såg nu att du insett det själv)
Ja iofs, det är ju sant. :) tack!




