Ge ett exempel på delrum V och baser B och C sådan att P är basbytesmatrisen från B --> C

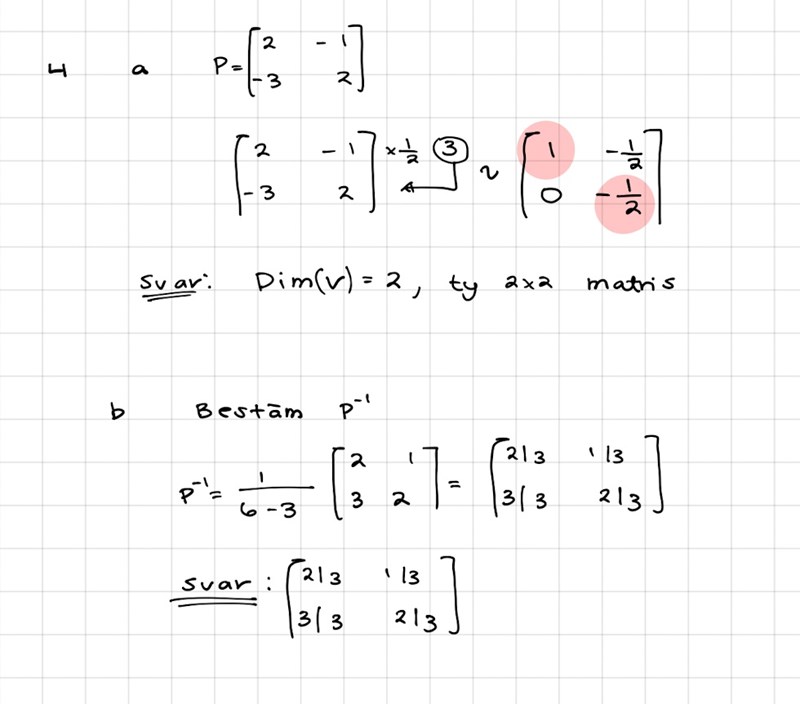 Jag förstår inte riktigt hur man ska göra fråga C, eller hur jag ska börja. Om man sätter exempelvis B=[2,-3], [-1,2] och beräknar då P^-1B=C=[1,0], [0,1], men vad blir då V?
Jag förstår inte riktigt hur man ska göra fråga C, eller hur jag ska börja. Om man sätter exempelvis B=[2,-3], [-1,2] och beräknar då P^-1B=C=[1,0], [0,1], men vad blir då V?
Ett tag sedan jag jobbade med linjär algebra.
Ett delrum V till R^3 innebär, om jag minns rätt, att det finns matriser som rymms i V men som inte fyller upp hela R^3. Om du förstår vad jag menar. Till exempel kan ett delrum V = alla symmetriska 2x2 matriser
Tänk på att det står . Så dina vektorer skall ha 3 koordinater, inte två.
Du kan tex välja två linjärt oberoende vektorer och (i ) som vektorerna i basen C. V blir då helt enkelt det linjära spannet av basen C, V = span(C).
Sedan kan man visa (gör det) att om vi vill att PB->C = P så ges basvektorerna i basen B enligt
, i = 1, 2.
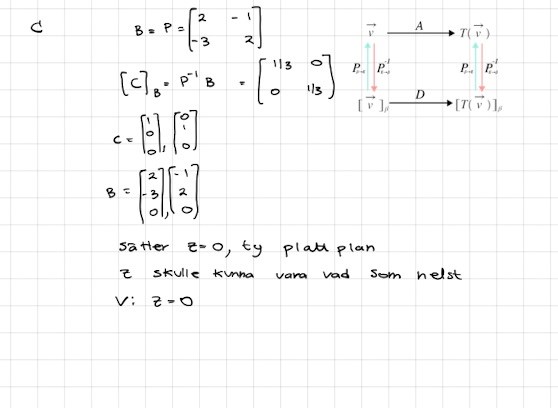
skulle detta funka?
Svaret är rätt. Men jag förstår inte riktigt din lösningsmetod.
b1 = P11c1 + P21c2 = =, check.
b2 = P12c1 + P22c2 = =, check.
Kan du förklara din lösningsmetod. Tex vad vill du säga med diagrammet?
Om vi i stället väljer V till att vara planet x + y + z = 0, hur löser du då problemet med din metod?
Det vi har gjort innan är att använda det som står i diagrammet för att lösa uppgifterna. Om vi har V och vill till Vb<-c så kan man väl bara ta övergångmatrisen P-1•B för att då C?

som på denna liksom
Men det är ju ett annat problem. Dvs att beskriva en avbildning S:s matris relativt olika baser. På vilket sätt menar du att detta har bäring på denna uppgift?
jag tänkte att man skulle tänka ungefär lika, men att man inte ska gå till standardbasen, utan att man ska gå från en basa till den andra direkt
Det skulle kanske fungera om vi hade att göra med basvektorer för R3, men nu är V ett delrum till R3 och standardbasen kanske inte ens ligger i V.
Tex om V är planet x + y + z = 0, så ligger ju ingen av vektorerna i standardbasen för R3 i V, så det ställer ju till det.
oh okay, men hur ska man tänka då?
Om du har två baser B = och C = för samma vektorrum så kan du alltid uttrycka vektorerna i den ena basen med linjärkombinationer av vektorerna i den andra basen på ett unikt sätt, per definition av vad som menas med en bas.
Dvs det finns således en unik 2 x 2 matris R sådan att
Vi har även basbytesmatriser som beskriver hur en vektors koordinater i en av baserna relateras till vektorns koordinater i den andra basen.
.
Här betecknar en kolonnmatris med vektorn :s koordinater relativt basen X. Jag antar att den notationen är känd. PB->C är basbytesmatrisen från B till C.
Jag hävdar nu att R = . Visa att detta stämmer.
alltså jag förstår inte riktigt vad du menar, när vi tar P-1B=blir det ju samma sak som c1= P-111b1+P-121b1=[1,0,0], och
c2=P-112b2+P-122b2=[0,1,0]. Funkar ite detta alltid?
OK, jag tror jag förstår vad du menar nu.
Det som gäller, med vektrisnotation, är
Så om vi väjer ”B” = så kan vi räkna ut ”C” som
C = = =.
Kan du nu lösa problemet om vi i stället väljer V som planet x + y + z = 0?
Hej, här är mitt försök till att lösa din fråga. Är detta rätt eller ska man tänka på något annat sätt?
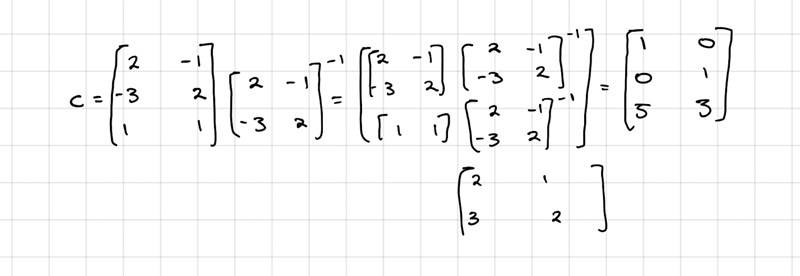
Det blir inte riktig rätt. Vektorn ligger inte i planet x + y + z = 0. Kan du modifiera den lite så att du får en vektor i planet?
okej, då förstår jag. Vektorn [-1,2-,1] ligger ju i planet och då blir det såhär: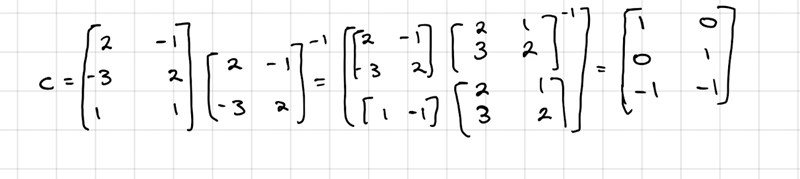
Det verkar ge ett rimligt svar. Vektorerna i C ligger i planet och är linjärt oberoende, och således en bas för planet.
Vidare så har vi
, så det hela stämmer. Check!
så man ska alltid dubbelkolla så att vektorerna uppfyller planets ekvation för att de ska vara en del av delrummet V?
En bas, för vilket delrum V som helst, måste alltid ligga i delrummet, annars har något gått fel.
Man skall alltid ta för vana att dubbelkolla att de svar man får fram verkar rimliga.

