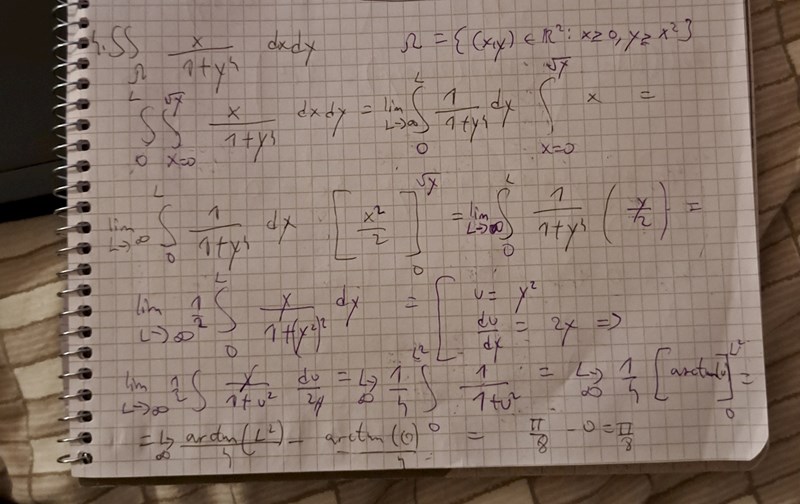Generaliserad integral

Variablerna har endast nedre begränsningar enligt $\Omega$. De övre är $\infty$, och det är därför den är generaliserad. 

MrPotatohead skrev:

Variablerna har endast nedre begränsningar enligt $\Omega$. De övre är $\infty$, och det är därför den är generaliserad. 

Hur ska man avgöra gränserna?  Jag kan tänka mig x går mellan 0 och inf pga x>=0 och y går från x^2 till inf. Men jag är inte helt säker på detta. 

Trinity2 skrev:

Visa spoiler

Måste man göra variabelbyte eller funkar det utan och ändå få samma svar?

destiny99 skrev:

Trinity2 skrev:

Visa spoiler

Måste man göra variabelbyte eller funkar det utan och ändå få samma svar?

Nej, man kan se det direkt men det brukas uppskattas att man är tydlig här på PA

Trinity2 skrev:

destiny99 skrev:

Visa föregående citat

Trinity2 skrev:

Visa spoiler

Måste man göra variabelbyte eller funkar det utan och ändå få samma svar?

Nej, man kan se det direkt men det brukas uppskattas att man är tydlig här på PA

Hur menar du att man kan se det? Jag tror jag förstår varför du inför H och M för båda ska ju gå mot oändligheten. 

Hej igen!

Jag försökte med gränserna för x och y men det verkar inte gå så bra tyvärr. Jag tittade även på din bild men jag ser liksom inte hur du gör när du väljer x och y gränserna. Det känns som att jag missar detaljer eller liknade. Jag skulle behöva lite mer hjälp med dem samt hur man integrerar 1/(1+y^4) som såg fruktansvärt svårt ut. 

destiny99 skrev:

Hej igen!

 

Jag försökte med gränserna för x och y men det verkar inte gå så bra tyvärr. Jag tittade även på din bild men jag ser liksom inte hur du gör när du väljer x och y gränserna. Det känns som att jag missar detaljer eller liknade. Jag skulle behöva lite mer hjälp med dem samt hur man integrerar 1/(1+y^4) som såg fruktansvärt svårt ut. 

Integrera 1/(1+y^4) går men är för svårt när det finns enklare väg.

Trinity2 skrev:

destiny99 skrev:

Hej igen!

 

Jag försökte med gränserna för x och y men det verkar inte gå så bra tyvärr. Jag tittade även på din bild men jag ser liksom inte hur du gör när du väljer x och y gränserna. Det känns som att jag missar detaljer eller liknade. Jag skulle behöva lite mer hjälp med dem samt hur man integrerar 1/(1+y^4) som såg fruktansvärt svårt ut. 

Integrera 1/(1+y^4) går men är för svårt när det finns enklare väg.

Tydligen kan man använda t=y^2 och köra  därifrån. Jag förstod också varför man ska ha de gränserna som du hade .

Det är ingen bra metod, mycket kan gå fel på vägen.

Här är svaret om du vill prova

Trinity2 skrev:

Det är ingen bra metod, mycket kan gå fel på vägen.

Här är svaret om du vill prova

Jag tror du missförstod mig lite. Jag syftar på att sätta u=y^2 och sen blir det arctan när man integrerar med nya gränser. Jag fick pi/8. Kan skicka hur jag gjort samt facits svar. 

destiny99 skrev:

hur man integrerar 1/(1+y^4) som såg fruktansvärt svårt ut.

Fyi är nog det ”enklaste” sättet att integrera $\frac{1}{x^4+1}$ är att faktorisera $x^4 +1$ till två andragradspolynom och sedan göra en partiell bråkuppdelning. 

Det är dock en ganska besvärlig integral att beräkna (om den inte är bestämd och går från 0 till $\infty$. Då kan man utnyttja andra knep).

Tillägg: 28 maj 2025 15:31

Man kan exempelvis faktorisera $x^4+1$ med hjälp av konjugatregeln:

$x^4 + 1 = x^4 + 2x^2 + 1 -2x^2 = (x^2+1)^2-2x^2 = (x^2+1+x\sqrt 2)(x^2+1-x\sqrt 2)$

$x^4 + 1 = (x^2+x\sqrt 2+1)(x^2-x\sqrt 2+1)$

Eller genom att hitta rötterna till polynomet och konstruera två reella andragradspolynom genom att para ihop konjugaten.