15 svar

322 visningar

dajamanté är nöjd med hjälpen

Generaliserade konjugat regel

Tack för flera mycket intressant tråd igår om den generaliserade konjugat regeln.

Jag försökte öva i morse med det, nämligen med bevis, som skulle bevisas som en geometrisk summa: $(a - b) \sum_{k = 0}^{n - 1} a^{(n - 1) - k} b^{k}$

Den enda jag lyckades göra så länge är att testa om det fungerar (det är klart att det funkar utmärkt men ibland måste man se det med sina egna trötta ögon).

Angående bevis:

En geometrisk summa bevisas med att utveckla en lista, multiplicera lista med första termen och subtrahera $L_{2}$ - $L_{1}$ . I detta fall: bör jag multiplicera med $a$ eller $b$ ? Eller $(a-b)$

Jag misstänker att svaret är $b$ eftersom den börjar med faktor noll?

Blir det något som:

$L_{2} = b \times (a^{n - 1 - k} b^{k} + a^{n - 1 - (k + 1)} b^{(k + 1)} . . . + a^{k} b^{n - 1 - k}) \Leftrightarrow a^{n - 1 - k} b^{k + 1} + a^{n - 1 - (k + 1)} b^{(k + 2)} . . . + a^{k} b^{n - 1 - (k + 1)} L_{2} - L_{1} = a^{n - 1 - k} b^{k + 1} + a^{n - 1 - (k + 1)} b^{(k + 2)} . . . + a^{k} b^{n - 1 - (k + 1)} - a^{n - 1 - k} b^{k} + a^{n - 1 - (k + 1)} b^{(k + 1)} . . . + a^{k} b^{n - 1 - k}$

Därifrån vet jag inte vad jag ska ta bort direkt för att utföra subtraktionen. Jag ser bara mycket håriga exponenter!

Bilda två listor av din summa, $aL$ och $bL$ . Sätt summorna ovanför varandra och se vilka termer som tar ut varandra när du bildar $(a-b)L=aL-bL$ .

$\begin{array}{lcccccccccccc}a^{n}& + & a^{n-1}b & + & a^{n-2}b^2 & + & ... & + &ab^{n-1} & & \\ & & a^{n-1}b & + & a^{n-2}b^2 & + & a^{n-3}b^3 & + & ... & + &b^n & &\\\end{array}$

Kvar blir

$a^n-b^n$

Hej!

Om du bryter ut $a^{n-1}$ så kan summan skrivas

$a^{n-1}(1+k+k^2+\cdots+k^{n-1})$

där kvoten $k=\frac{b}{a}$ . Den geometriska summan är lika med

$\frac{k^n-1}{k-1}$

och $k-1=\frac{b-a}{a}$ samt $k^n-1=\frac{b^n-a^n}{a^n}$ så att den geometriska summan kan skrivas

$\frac{b^n-a^n}{a^(n-1)}\ .$

Därmed är "beviset" klart.

Albiki

Hej!

Det ska stå att den geometriska summan är lika med

$\frac{b^n-a^n}{a^{n-1}}$ .

Albiki

Hej Albiki,

Jag tror att du har slarvat bort $(b-a)$ Med dina beteckningar blir

$\frac{k^n-1}{k-1}=\frac{a^n-b^n}{(a-b)a^{n-1}}$

vilket när man multiplicerar tillbaka $a^{n-1}$ som du bröt ut samt multiplicerar summan med (a-b) ger regeln

$\displaystyle{ (a-b)\sum_{k=0}^{n-1} a^{(n-1)-k}b^k=a^n-b^n}$ .

Guggle skrev :
Bilda två listor av din summa, $aL$ och $bL$ . Sätt summorna ovanför varandra och se vilka termer som tar ut varandra när du bildar $(a-b)L=aL-bL$ .
Kvar blir
$a^n-b^n$

Vi kom fram till:

$(a - b) L = a L - b L = (a - b) L = a^{n} - b^{n}$

Varför blir inte L:

$L = \frac{a^{n} - b^{n}}{(a - b)}$

Alltså varför listan delas inte med (a-b)?

Riktigt dum fråga nu:

Varför börjar listan med $a^{n}$ och inte $a^{n - 1}$ ?

Jo, jag är fortfarande mycket obekväm med summa tecken. Man kan även säga rädd.

dajamanté skrev :

Riktigt dum fråga nu:
Varför börjar listan med an och inte an-1?
Jo, jag är fortfarande mycket obekväm med summa tecken. Man kan även säga rädd.

Det kan hända att vi menar olika saker med L och att jag förvirrade dig. Jag tänkte mig L som summan, så här:

$\displaystyle L=\sum_{k=0}^{n-1}a^{(n-1)-k}b^k$

Nu kan vi titta på vilka element som ingår i listan. Det första elementet är (k=0) är $a^{(n-1)-0}b^{0}=a^{n-1}$ .

Det andra elementet (k=1) är $a^{(n-1)-1}b^{1}=a^{n-2}b$ .

Skriver vi ut några element till får vi listan :

$L=\begin{array}{rrrrrrrrrrrrr}a^{n-1} & + & a^{n-2}b & + & a^{n-3}b^2 & + & a^{n-4}b^3 & + & ... & + &b^{n-1} & & \end{array}$

Multiplicerar vi listan med a får vi

$L_a=\begin{array}{rrrrrrrrrrrrr}a^{n} & + & a^{n-1}b & + & a^{n-2}b^2 & + & a^{n-3}b^3 & + & ... & + &ab^{n-1} & & \end{array}$

Skulle vi istället multiplicera (den ursprunliga) listan med b får vi

$L_b=\begin{array}{rrrrrrrrrrrrr}a^{n-1}b & + & a^{n-2}b^2 & + & a^{n-3}b^3 & + & a^{n-4}b^4 & + & ... & + &b^{n} & & \end{array}$

Att bilda $(a-b)L=aL-bL$ är alltså att beräkna $L_a-L_b$ , och när vi jämför listorna ser vi att vi kan stryka alla termer utom $a^n-b^n$ .

Nu kommer du att tro att jag ramlade på huvudet och har inte återfått medvetande sedan dess men... Var har $(a-b)$ försvunnit? Åtminstone förstår jag att $a^{n}-b^{n}$ är kvar :)

dajamanté skrev :
Nu kommer du att tro att jag ramlade på huvudet och har inte återfått medvetande sedan dess men... Var har $(a-b)$ försvunnit? Åtminstone förstår jag att $a^{n}-b^{n}$ är kvar :)

Vi multiplicerar in a och b i summorna, därför verkar de "försvinna". Från början är L bara summan

$L=\begin{array}{rrrrrrrrrrrrr}a^{n-1} & + & a^{n-2}b & + & a^{n-3}b^2 & + & a^{n-4}b^3 & + & ... & + &b^{n-1} & & \end{array}$

Sedan multiplicerar vi med a. Jag kallar alltså produkten $a\cdot L$ för $L_a$ .

$L_a=\begin{array}{rrrrrrrrrrrrr}a^{n} & + & a^{n-1}b & + & a^{n-2}b^2 & + & a^{n-3}b^3 & + & ... & + &ab^{n-1} & & \end{array}$

Är du med på det?

So far so good.

$a L = L_{a}$ . Inga konstigheter.

$b L = L_{b}$

Det ör nog inga konstigheter heller.

Var jag börjar bli blind är där:

$L_{a} - L_{b} = L (a - b) = a^{n} - b^{n}$

dajamanté skrev :
So far so good.
$a L = L_{a}$ . Inga konstigheter.
$b L = L_{b}$
Det ör nog inga konstigheter heller.

Var jag börjar bli blind är där:
$L_{a} - L_{b} = L (a - b) = a^{n} - b^{n}$

Om $L_a=a\cdot L$ och $L_b=b\cdot L$ så är

$(a-b)\cdot L= L\cdot (a-b)=L\cdot a-L \cdot b=L_a-L_b$

Distributiva lagen $a(b+c)=ab+ac$ . Om du vill kan du dra pilar under för att multiplicera in L i parentesen.

Om du skriver upp $L_a$ och $L_b$ ovanför varandra och stryker gemensamma termer ser du att det som blir kvar av $L_a-L_b$ är $a^n-b^n$ , dvs den första termen i $L_a$ och den sista termen i $L_b$ . De enda två termer som inte tar ut varandra.

Jo, det är jag med! Vad jag är inte med är varför (a-b) delar inte ut a^n-b^n om vi vill få fram L.

Alltså varför den ros parentes hoppar inte under a^n-b^n?

Jag kan sluta fråga om du tycker att det är super stupid. Jag kanske kommer på det mitt i natten.

dajamanté skrev :
Jo, det är jag med! Vad jag är inte med är varför (a-b) delar inte ut a^n-b^n om vi vill få fram L.
Alltså varför den ros parentes hoppar inte under a^n-b^n?

Hmm. Fast det blir ju en (a-b) kvar? Du är med på att

$L=\displaystyle \sum_{k=0}^{n-1} a^{(n-1)-k}b^k=\frac{a^n-b^n}{(a-b)}$

Det vi vill "bevisa" är att (titta på ditt första inlägg)

$(a-b)\cdot L=(a-b)\displaystyle \sum_{k=0}^{n-1} a^{(n-1)-k}b^k=a^n-b^n$

Jag har svårt att förstå vad du frågar. Kanske kan du visa med ett exempel hur du menar att (a-b) ska hoppa på $a^n-b^n$ ?

Nu är jag med!

Delen jag menade är denhär:

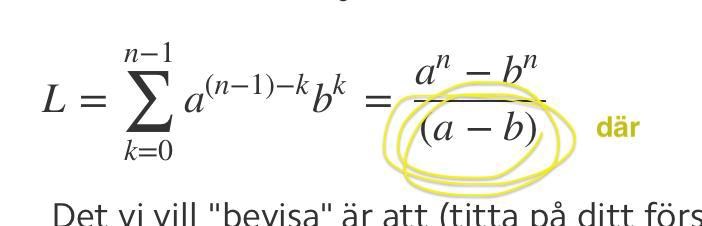
Jag förstådd inte var den var i din tidigare inlägg, för det står :

Kvar blir

$a^n-b^n$

Guggle skrev :
Bilda två listor av din summa, $aL$ och $bL$ . Sätt summorna ovanför varandra och se vilka termer som tar ut varandra när du bildar $(a-b)L=aL-bL$ .
$\begin{array}{lcccccccccccc}a^{n}& + & a^{n-1}b & + & a^{n-2}b^2 & + & ... & + &ab^{n-1} & & \\ & & a^{n-1}b & + & a^{n-2}b^2 & + & a^{n-3}b^3 & + & ... & + &b^n & &\\\end{array}$
Kvar blir
$a^n-b^n$

Förresten, vad är lcccccccccccc i din latex?

dajamanté skrev :
Nu är jag med!

Jaa, bra! GULDSTJÄRNA!

Förresten, vad är lcccccccccccc i din latex?

Jo, när man skriver summor så blir det tydligare om man har lite mellanrum mellan termerna och dessutom låter termer som är "samma" stå rakt under varandra, Därför valde jag att sätta dem i en ordnad array.lcr Avgör om kolonnen ska höger-, mitten- eller vänsterjusteras.

(l)eft

$\begin{array}{l|r|r|}a & b & c\\a+b & b & c\end{array}$

(c)enter

$\begin{array}{c|r|r|}a & b & c\\a+b & b & c\end{array}$

(r)ight

$\begin{array}{r|r|r|}a & b & c\\a+b & b & c\end{array}$

Guggle skrev :
dajamanté skrev :
Nu är jag med!
Jaa, bra! GULDSTJÄRNA!

Lol... Shametjärna menar du...

Förresten, vad är lcccccccccccc i din latex?
Jo, när man skriver summor så blir det tydligare om man har lite mellanrum mellan termerna och dessutom låter termer som är "samma" stå rakt under varandra, Därför valde jag att sätta dem i en ordnad array.lcr Avgör om kolonnen ska höger-, mitten- eller vänsterjusteras.
(l)eft
$\begin{array}{l|r|r|}a & b & c\\a+b & b & c\end{array}$
(c)enter
$\begin{array}{c|r|r|}a & b & c\\a+b & b & c\end{array}$
(r)ight
$\begin{array}{r|r|r|}a & b & c\\a+b & b & c\end{array}$

Det måste jag jobba på...

Svara Avbryt

Visa senaste svar