Genom vilken sluten yta S är flödet av vektorfältet maximalt? Beräkna det maximala flödet
 Hej!
Hej!
Jag har problem med denna uppgift och vet inte hur man ska komma igång.
Börja med att skriva fi i sfäriska koordinater. Beräkna sedan grad(fi).
PATENTERAMERA skrev:Börja med att skriva fi i sfäriska koordinater. Beräkna sedan grad(fi).
Men är det inte bättre att kalla phi för R^2=x^2+y^2+z^2 som är ett sfär med radie R? Känns som mer jobb att skriva phi i sfäriska koordinater. Då kan man använda gradphi för sfäriska koordinater för vi får phi(R)=a^2R-R^4
Du skrev ju fi i sfäriska koordinater. Vad blir grad(fi)?
PATENTERAMERA skrev:Du skrev ju fi i sfäriska koordinater. Vad blir grad(fi)?
Du menar i #3?
PATENTERAMERA skrev:Ja.
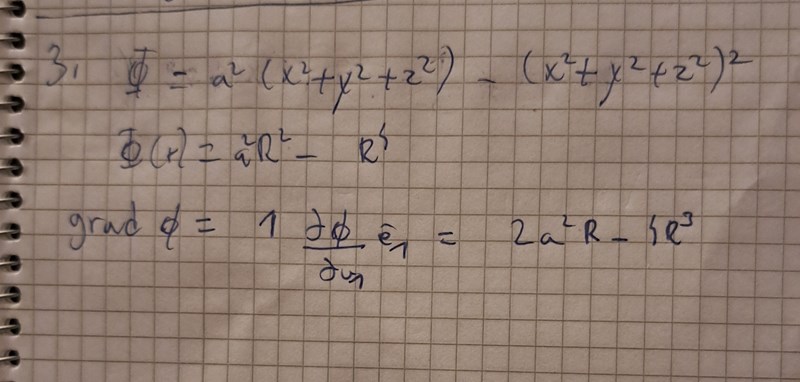
Det skall bli en vektor.
PATENTERAMERA skrev:Det skall bli en vektor.
Jag använde grad phi från formelsamlingen för vektoranalys.
Du glömde att ta med er.
Skissa vektorfältet och tänk lite på hur du skulle lägga en sluten yta för att flödet (ut) genom ytan skall bli så stort som möjligt.
PATENTERAMERA skrev:Skissa vektorfältet och tänk lite på hur du skulle lägga en sluten yta för att flödet (ut) genom ytan skall bli så stort som möjligt.
Jag kan tyvärr inte. Sitter på tåget. Återkommer om jag fått hjälp med uppgiften idag.


