Geogebra- få fram x
Hej, jag håller på med den här uppgiften.

 Uppgiften är att hitta intervallet så det blir symmetriskt bredvid väntevärdet. (om det är dåligt förklarat förklarar nog uppgiften bättre).
Uppgiften är att hitta intervallet så det blir symmetriskt bredvid väntevärdet. (om det är dåligt förklarat förklarar nog uppgiften bättre).
Då tänkte jag att integralen från - oändligheten till ett x-värde = 0,25 (se bild).
Jag fick fram x=48 genom att kolla på facit. Finns det något sätt att få fram x i geogebra utan att behöva gissa sig fram? Jag försökte med g=0,25 men då försvann min integral.
Jag kan ej Geogebra men troligen skall du göra övre integrationsgränsen som en "slider" med 50±6 och variera tills du får integralens värde till 0.25.
Du bör få runt 47.9765 ≈ 48 dvs -2 från 50 varför ditt intervall är 50±2=[48,52].
Om jag förstår det rätt måste jag fortfarande testa mig fram.
Vet du hur man gör det i Desmos?
Jag gjorde en enkel "model" i Geogebra
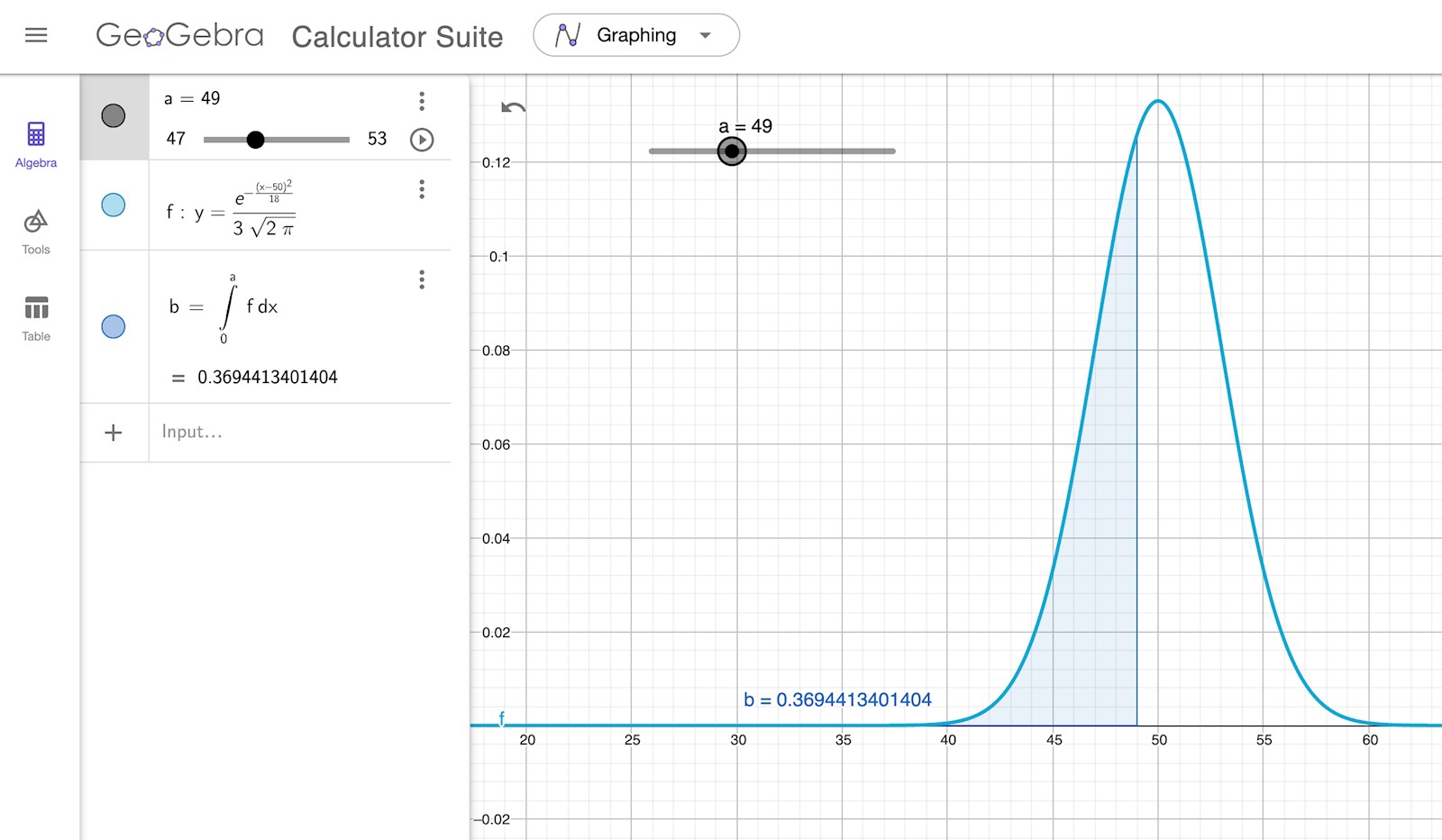
genom att variera a får jag
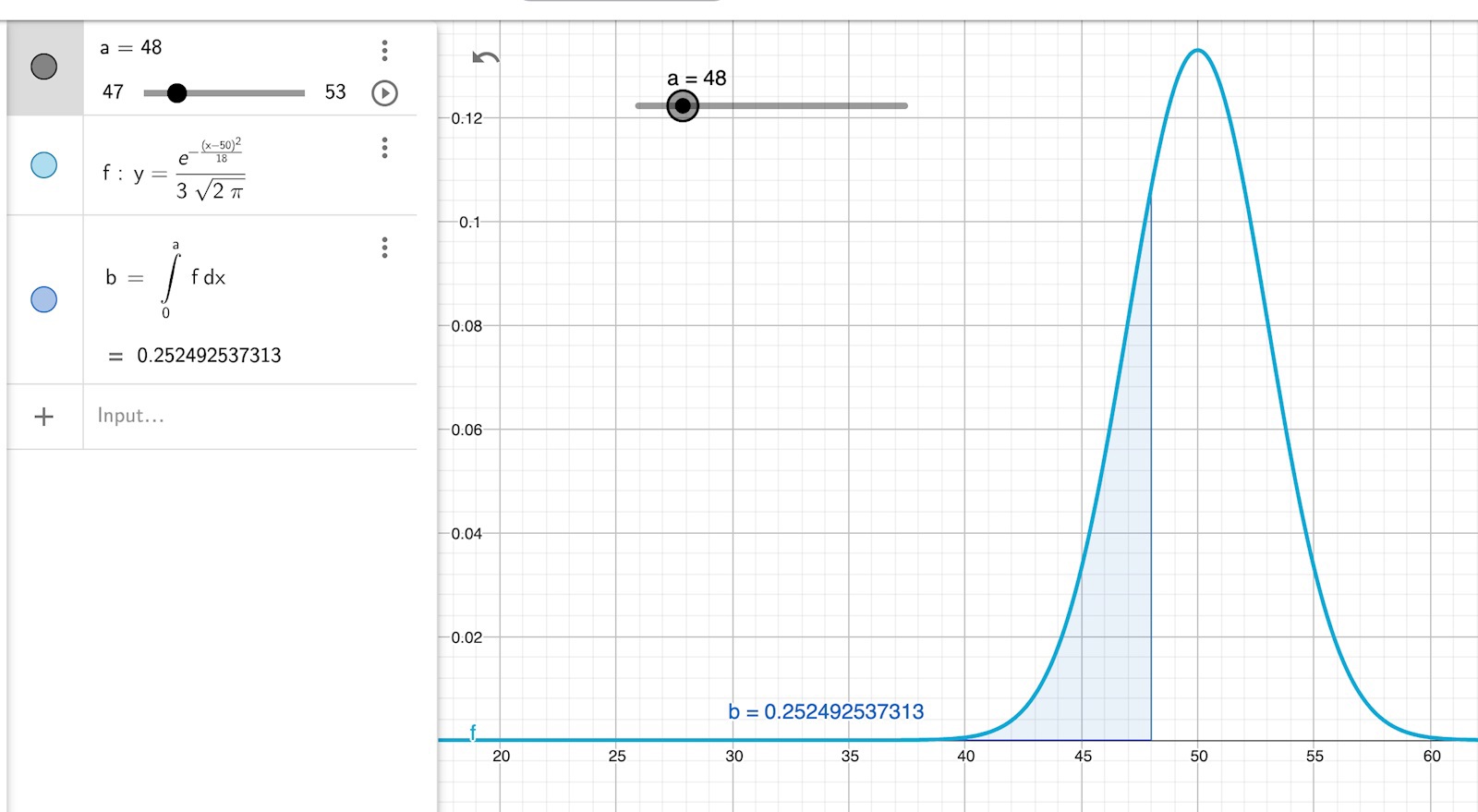
Undre gränsen behöver ej vara -oo, funktionen ->0 så snabbt att 0 duger bra. Jag provade med -oo men då beräknades ej integralen. Av någon anledning blir integralen 0 om man anger -1000 men beräknad för -10. Hm? Konsigt. Men 0 funkar bra i detta fall.
Så slutsatsen är att jag måste prova mig fram?
Hur får jag den blåa delen att synas i geogebra. Jag försökte men då för jag en graf.
Hejsan266 skrev:Hur får jag den blåa delen att synas i geogebra. Jag försökte men då för jag en graf.
Ja, man får prova sig fram.
Den kom automagiskt när man skrev in integralen.
Man kan titta i en tabell också.
https://www.maths.lth.se/matstat/kurser/tabeller/tabeller.pdf
Här är en tabell men jag förstår inte riktigt hur och var jag ska läsa av den.
Tabellen börjar på 0,5, så om jag tänker rätt ska du söka upp värdet 0,75. Det är ungefär halvvägs mellan 0,67 och 0,68.
0,67 * 3 är ungefär 2.
Man kan interpolera bättre i tabellen, men vi har ju ändå bara en siffras noggrannhet i standardavvikelsen.


