Geometri

Hejsan! Har ingen aning om hur man löser denna, känns som man har för få värden, åtminstone när jag försökte…
Du skulle kunna börja med att ta reda på vad höjden av de skuggade areorna är. I triangeln till vänster så har den skuggade arean höjden (h - 11), och i triangeln till höger har den skuggade arean höjden (h - 5).
Givetvis, men därefter? Jag får fram en ekvation med alldeles för många variabler…
Om du inte redan har provat, så skulle du kunna testa att använda likformighet. Till exempel så är den skuggade delen till höger likformig med triangeln ABC.
Lasse Vegas skrev:Om du inte redan har provat, så skulle du kunna testa att använda likformighet. Till exempel så är den skuggade delen till höger likformig med triangeln ABC.
Topptriangel. Jag har verkligen ingen aning hur man fortsätter därifrån.
Det finns minst två sätt att lösa uppgiften.
1. Kalla AC för b. Använd likformighet för att skriva uttryck för respektive transversal.
Visa spoiler
Den vänstra har längden 11b/h
Sedan kan du skriva uttryck för respektive grå area (använd formeln för parallelltrapetsens area för den vänstra) och få en ekvation. b försvinner på vägen.
2. Använd att areaskalan är kvadraten på längdskalan.
Kalla ABC:s area för A och de grå (lika stora) områdena för Agrå.
Du kan nu ställa upp två ekvationer som kan sättas ihop till en.
Sätt olika rubriker på dina geometrifrågor så det går att skilja dem åt.
Vad betyder 11b/h? Själv upplever jag att det ger sidan längst upp i den skuggade parallelltrapetsen.
Alltså är ekvationen för den skuggade trapetsen:
(h-11)((11b/h)+b)*0.5
Ekvationen för den skuggade triangeln blir:
(h-5)*(5b/h-11)*0.5
Stämmer detta? Har lagt in det i en ekvationslösare och det ger konstiga värden, hur fortsätter jag härifrån?
Om vi kallar transversalen i vänstra figuren x och i högra figuren y har vi
x/b = 11/h; x = 11b/h
Det är vad du använt i ditt helt riktiga uttryck (ingen ekvation) för trapetsets area.
y/b = (h-5)/h; y = b(h-5)/h
Kolla igen vad det blir för uttryck för triangelarean.
varför tar du höjd dividerat med bas? Är det någon vanlig princip inom likformiga trianglar?
Vilken del av räkningarna syftar du på?
”x/b = 11/h; x = 11b/h”
Förresten:
Vilken transversal är det du menar i bilden?

En transversal är en linje som skär andra linjer.
Här bara linjen som betecknats med x.
Basen i topptriangeln/basen i stora triangeln = höjden i topptriangeln/höjden i stora triangeln.

Louis skrev:En transversal är en linje som skär andra linjer.
Här bara linjen som betecknats med x.
Basen i topptriangeln/basen i stora triangeln = höjden i topptriangeln/höjden i stora triangeln.
Uppfattat, förstod bara inte vilken transversal du syftade på 😅
Nu har jag två uttryck:
(h-11)((11b/h)+b)*0.5
för trapetsen och:
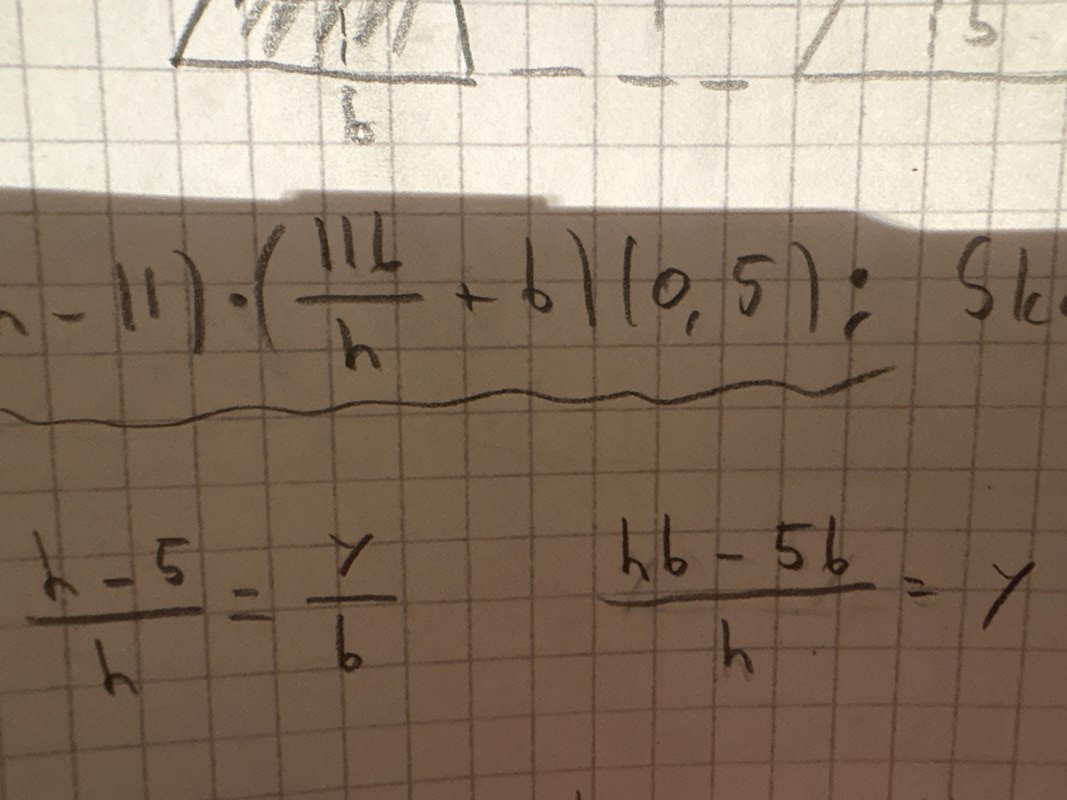
Råkade skriva fel i Pluggakuten….
Det första stämmer.
b(h-5)/h är basen i den grå triangeln. Behåll b utanför parentesen för den faktorn kommer försvinna när du ställer upp ekvationen.
Men yh/b förstår jag inte. y var en tillfällig beteckning på basen.
Som ska multipliceras med höjden (h-5).
Alltså för den grå triangeln.
Nu kan du sätta uttrycken lika med varandra.

