Geometri

Använd dig av vinkelsumman för figurerna! Om du inte vet hur stor vinkelsumman är, kan du dela upp den i trianglar: 

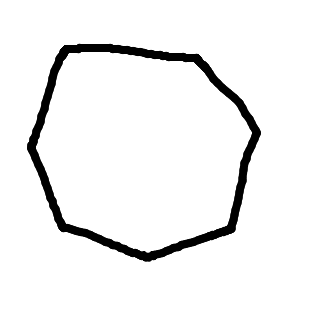
Dela upp månghörningen i delar:

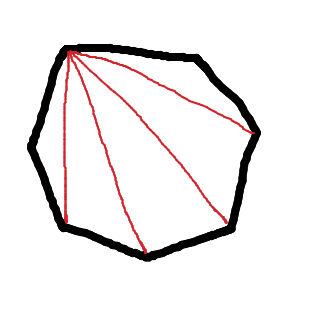
En heptagon kan delas in i sju trianglar, som alla har vinkelsumman $180^\circ$. Därmed har en heptagon vinkelsumman $180^\circ\cdot5=900^\circ$. :)

Tack!

Varsågod! :)

Jag har kommit så långt att jag fått fram att vinkelsumman blir 540. Svaret skall vara 72 på a, men jag förstår fortfarande inte hur?

Frida14 skrev:

Jag har kommit så långt att jag fått fram att vinkelsumman blir 540. Svaret skall vara 72 på a, men jag förstår fortfarande inte hur?

Vi har att vinkelsumman är 540 , vi har 5 vinklar i en pentagon.

Dela upp 540 på 5st vinklar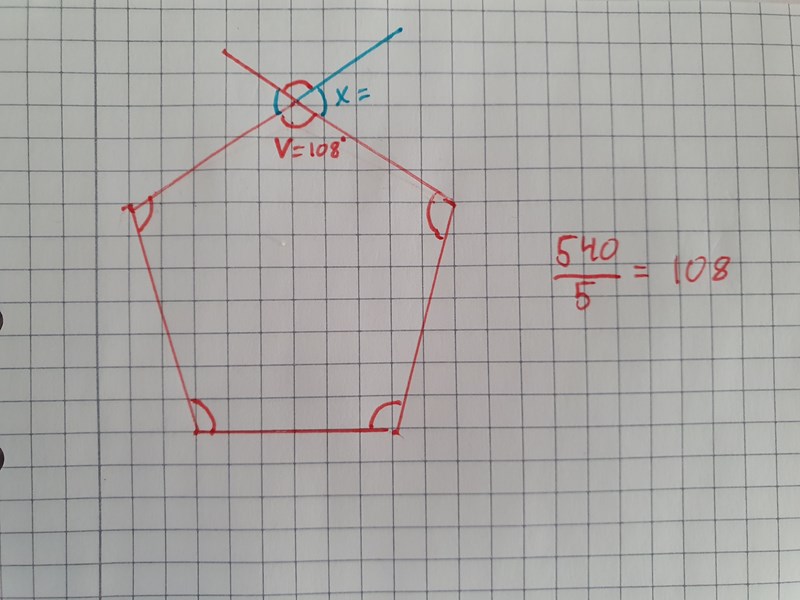

kommer du vidare här ?

Jag kom fram till svaret 108... skall tänka lite till

Nej, jag förstår inte alls.:(

Tänk dig en myra som bara kan gå längs räta linjer.
Låt den börja t ex i nedre vänstra hörnet på femhörningen i a) och gå snett uppåt vänster.

När den kommer till nästa hörn, tar den till höger, och följer nästa sida, snett uppåt höger.
När den kommit till toppen av figuren, blir den förvirrad,
men väljer att även här ta till höger, och följa nästa sida, snett nedåt höger.

Den får då veta att den just har vridit sig  x° åt höger (det står i figuren).

Myran stretar vidare. När den kommer till nästa hörn, tar den till höger där också.
Då märker den, att den även här måste vrida sig precis   x°  för att hamna rätt på  nästa sida.

Så småningom kommer den tillbaka till nedre vänstra hörnet, där den började.
När den då vridit sig  x° åt höger igen, känner den igen sig (hurra!)
och inser att den nu har vridit sig ett helt varv sedan den började promenaden.

Sedan rundturen började, har myran i varje hörn vridit sig  x° åt samma håll.
Det är fem hörn i figuren och nu har den vridit sig ett helt varv.

Men myran har glömt hur många grader det går på ett varv...

Hjälp myran!
 

Frida14 skrev:

Nej, jag förstår inte alls.:(

Cirkeln som skapades i toppen av min bild ovan har 360 grader som vinkelsumma. 

Vi vet att en vinkel v i cirkeln är 108 grader(den röda sidan), motstående röda vinkel är lika stor den.

108+108 = 216.

Den sökta vinkeln x kommer också ha en motstående vinkel som är exakt lika stor.

Tusen tack, hade inte kunnat tänka ut den själv. Jag förstår iallafall nu!!

Bra!
Följ myran i mitt inlägg för ett annat sätt att resonera.

Volens27 skrev:

Frida14 skrev:

Jag har kommit så långt att jag fått fram att vinkelsumman blir 540. Svaret skall vara 72 på a, men jag förstår fortfarande inte hur?

Vi har att vinkelsumman är 540 , vi har 5 vinklar i en pentagon.

Dela upp 540 på 5st vinklar

kommer du vidare här ?

Ok istället för att jag gör min egna tråd frågar jag bara här, varför dela på 5? Förstår inte riktigt..

För att pentagonen har fem vinklar:)

Frida14 skrev:

För att pentagonen har fem vinklar:)

Jo men varför är den informationen relevant? Trodde det bara var 900-360=540 och man var klar där liksom. Varför måste man dela 540 på fem för att det finns fem sidor i en Pentagon? 

För att lösa den här uppgiften behöver man veta hur stor var och en av vinklarna i en regelbunden femhörning är.

Myran klarar det ändå, om den bara får veta hur många grader det går på ett helt varv.  :-)