Geometri, delning av diagonal i ett parallelogram
Hej igen!
Jag har återigen stött på ett klurigt geometriproblem ( det sista av alla till och med! ), och det finns säkert en väldigt enkel metod att lösa problemet, dock har jag svårt att se hur jag skall gå till väga.
Det är återigen så att jag mest behöver ett tips på hur man skall angripa uppgiften då jag mest nu sitter och testar med att rita rätvinkliga trianglar till ingen nytta alls....
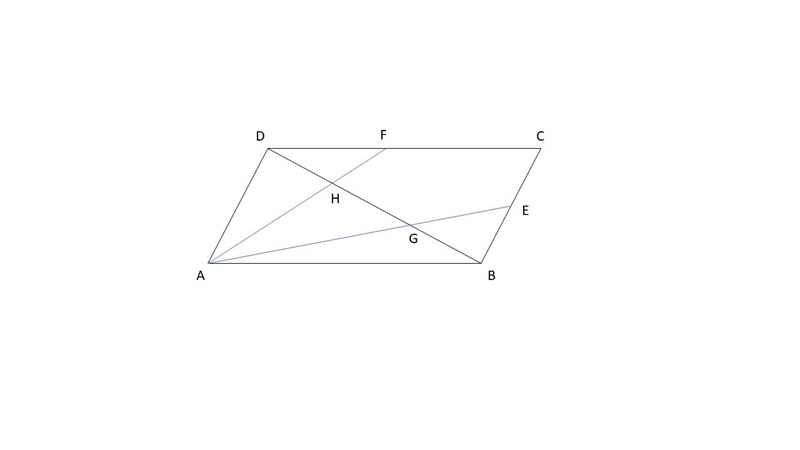
Uppgiften går då som följande ( trots att bilden var rätt dåligt ritad... ):
Låt punkten F vara mittpunkten på sträckan CD och låt punkten E vara mittpunkten på sträckan CB.
Visa att sträckorna AF och AE delar diagonalen (DB) i tre lika stora delar.
Notera ( Jag vet att det inte ser ut som att F är mittpunkten på bilden, men så äre det iaf!, man får stå ut med mitt dåliga ritande :P )
Nnotera att AHB och DHF är likformiga, med sidan DF motsvarande sidan AB (som ju har samma längd som CD). Fundera på om det kan leda till någon slutsats?
Det är bra med dåligt ritande, en av mina lärare sa en gång i tiden att "Geometri är konsten att dra korrekta slutsatser ur felaktiga bilder" :)
Som JohanB skriver "AHB och DHF är likformiga"
vilket gör alla kanter i AHB dubbelt så långa som i DHF
dvs DH är hälften av BH och därmed är DH 1/3 av DB.
Samma teknik på ADG som är likformig med EBG ger
att GB är 1/3 av DB.
Sådär, ledsen för "seg" respons.
Mycket smart idé att identifiera likformigheten, det var lite den hjälpen jag var ute efter.
Jag menar, om vi identifierar BHA och DHF som likformiga, och så identifierar vi ADG och EBG. som likformiga.
Då gäller, som larsolof skrev, att sidorna DH = BH / 2 , likväl som att BG = DG / 2.
Vi har alltså att DH = BH / 2.
Dessutom att BG = DG / 2.
Dock är jag inte helt säker på hur vi ur denna infromation kan dra slutsatsen att DH och BG respektive måste vara 1/3 av diagonalen DB... jag känner lite då att vi redan "utgått" ifrån att dom skall vara lika, vilket inte bevisar så mycket!
Oavsett är jag väldigt tacksam för alla hjälp :)!
Om 2HD=BH (enligt argument), och BD=BH+HD (vi delar upp sträckan i två delsträckor), hur många HD är BD?
Vi har alltså att DH = BH / 2 DH = 1/3 av DB
Dessutom att BG = DG / 2 BG = 1/3 av DB
1/3 1/3
+--------------------+--------------------+--------------------+
D H G B
Då måste HG vara återstående 1/3 av DB
2HD = BH, BD = BH + HD <=> BD = 3HD ... jaaaa ofc.
2BG = DG, BD = DG + BG => BD = 3BG
Eftersom HD = BD / 3 och BG = BD / 3 måste även HG = BD / 3 eftersom dom ligger på samma sträcka...
Nu föll äntligen poletten ner, tack som bara den :)!
Jag blir skyldig er båda en chokladkaka någon gång om vi av en slump träffas på ett fik :D


