Geometri uppgift

Feltänkt.

Louis skrev:

Feltänkt.

Tror jag inte. Det såg bra ut.

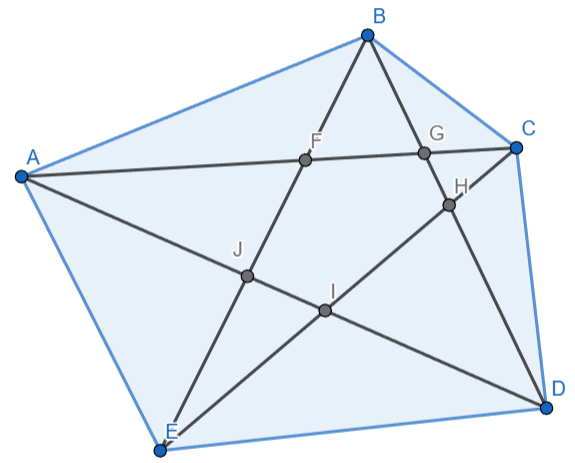
Först ritade jag en figur där det var uppenbart att
AC > AB
BD > BC
osv figuren runt.

Men om en vinkel är mycket spetsig stämmer det inte
på samma enkla sätt. Om man jämför sträckor i en annan ordning?

Louis skrev:

Först ritade jag en figur där det var uppenbart att
AC > AB
BD > BC
osv figuren runt.

Men om en vinkel är mycket spetsig stämmer det inte.

AI fann detta ....

Då femhöringen är konvex, så skär diagonalerna varandra.

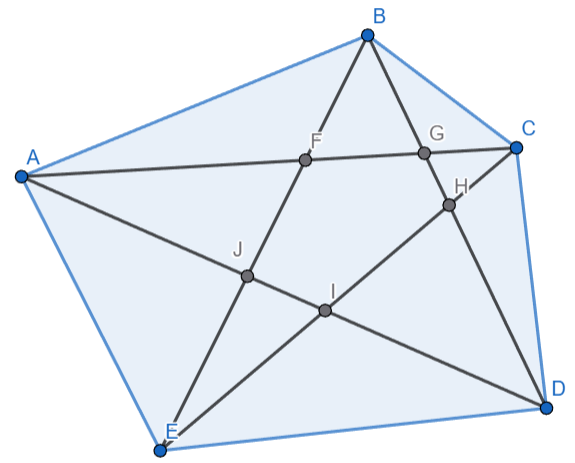
Enligt triangelolikheten är $AB < AF + FB$, $BC < BG+GC$ o.s.v.

Allt adderas ihop, så man får att

$AB + BC + CD + DE + EA < AF + FB + BG + GC + CH + HD + DI + IE + EJ + JA$

Sidorna i HL sorteras om:

$HL = \underbrace{(AF + GC)}_{< AC} + \underbrace{(FB + EJ)}_{< EB} + \underbrace{(BG + HD)}_{< BD} + \underbrace{(CH + IE)}_{< CE} + \underbrace{(DI + JA)}_{< DA}$.

Louis skrev:

Först ritade jag en figur där det var uppenbart att
AC > AB
BD > BC
osv figuren runt.

Men om en vinkel är mycket spetsig stämmer det inte
på samma enkla sätt. Om man jämför sträckor i en annan ordning?

En och en kan vilken som helst vara längst, men du jmf alltid 2 yttre sidor med en enda diagonal här, så då funkar triangelolikheten. 

LuMa07 skrev:

Då femhöringen är konvex, så skär diagonalerna varandra.

Enligt triangelolikheten är $AB < AF + FB$, $BC < BG+GC$ o.s.v.

Allt adderas ihop, så man får att

$AB + BC + CD + DE + EA < AF + FB + BG + GC + CH + HD + DI + IE + EJ + JA$

Sidorna i HL sorteras om:

$HL = \underbrace{(AF + GC)}_{< AC} + \underbrace{(FB + EJ)}_{< EB} + \underbrace{(BG + HD)}_{< BD} + \underbrace{(CH + IE)}_{< CE} + \underbrace{(DI + JA)}_{< DA}$.

Mycket fint, tack så mycket