Geometrisk talföljd sigma
Hej, jag förstår första uppgiften men inte andra, varför har de skrivit s6? Vi ska ju räkna s8 eller?
står inte det övre talet för antal element?
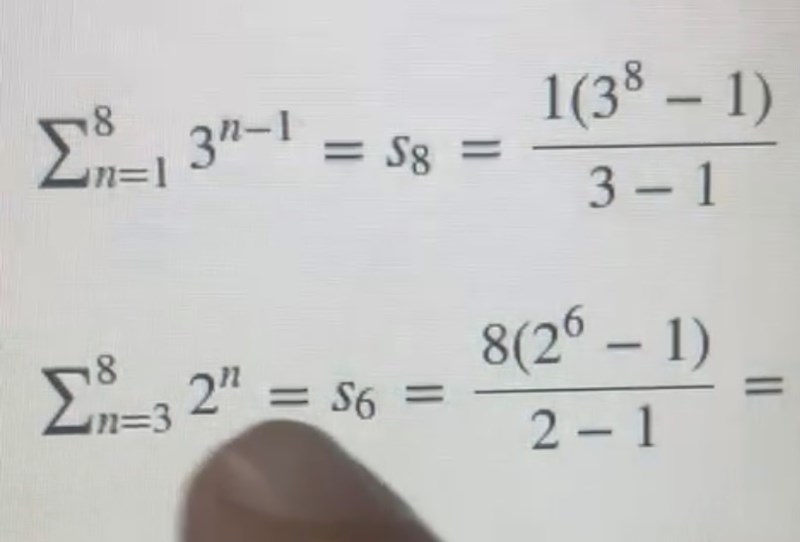
Det är 6 termer i summan, n=3, 4, 5, 6, 7, 8
ahaaa okej då förstår jag tack
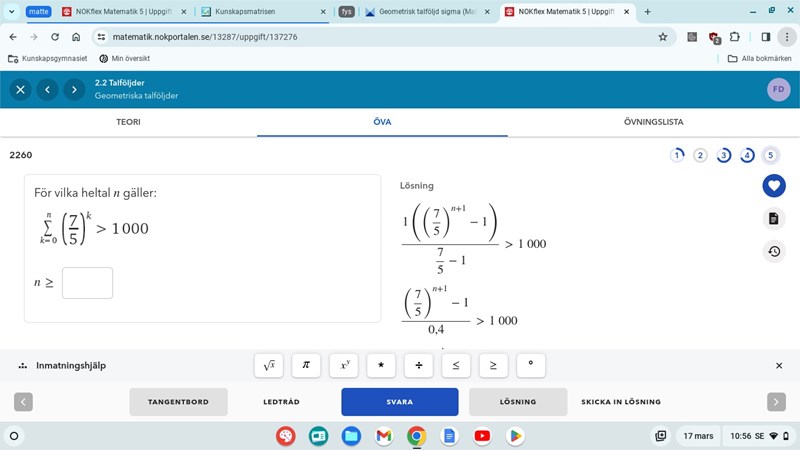
Här har man lagt att det ska vara sn+1
Hur har de fått det?

Vad är det som är sn+1?
Serien har n+1 termer. Är det svar på frågan?
men hur vet vi att den har n+1 termer? Jag tänkte att man skulle kanske lägga (7/5)^n
Det behöver vi egentligen inte veta, vi använder bara formeln för en geometrisk summa.
fast formeln för en geometrisk summa säger att det ska vara k^n inte k^n+1
Det beror på vad för summa man beräknar. Man kan låta summan börja på 0 eller på 1. Det blir olika formler.
så om den börjar på 0 så är det n+1 och om den börjar på 1 så är det n?
men varför?
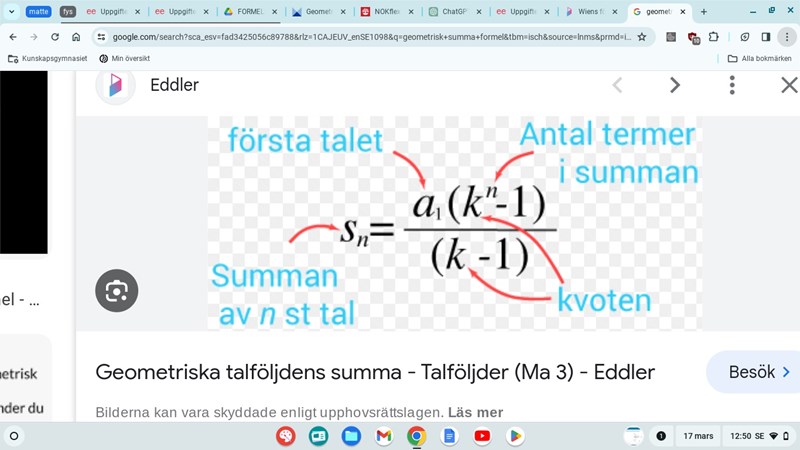
Hur ser den formel för geometrisk summa ut som du har sett?
Om k börjar på 1 och slutar på n så har summan n termer. Om den börjar på 0 och slutar på n så har den n+1 termer.
finns det någon förklaring till det
Om du har n glassar och jag ger dig en glass så har du n+1 glassar. Hur behövs det en förklaring?
finns det någon förklaring till det
Det är det som är det svåra med summor, man måste tänka jättenoga för att få med lagom många termer i summan, och det finns flera olika varianter av summaformeln, vilket verkligen inte underlättar!
okej tack