Geometriska problem
Jag behöver hjälp med uppgift 4333.
a) Jag förstår inte hur man kan se att trianglarna har ungefär samma storlek (area)? Jag ser att hypotenusan i ADP = lång katet i CPD, men f ö ser jag inga likheter? Hur kan AP vara lika lång som (c)?
b) Om jag ska kunna ett uttryck för y som innehåller c, måste jag väl anta att AP=c, men det är just det jag inte kan se?
Kan du ladda upp en bild på själva uppgiften?
 Hoppas bilden går att tolka, jag har inte tillgång till matteboken just nu!
Hoppas bilden går att tolka, jag har inte tillgång till matteboken just nu!
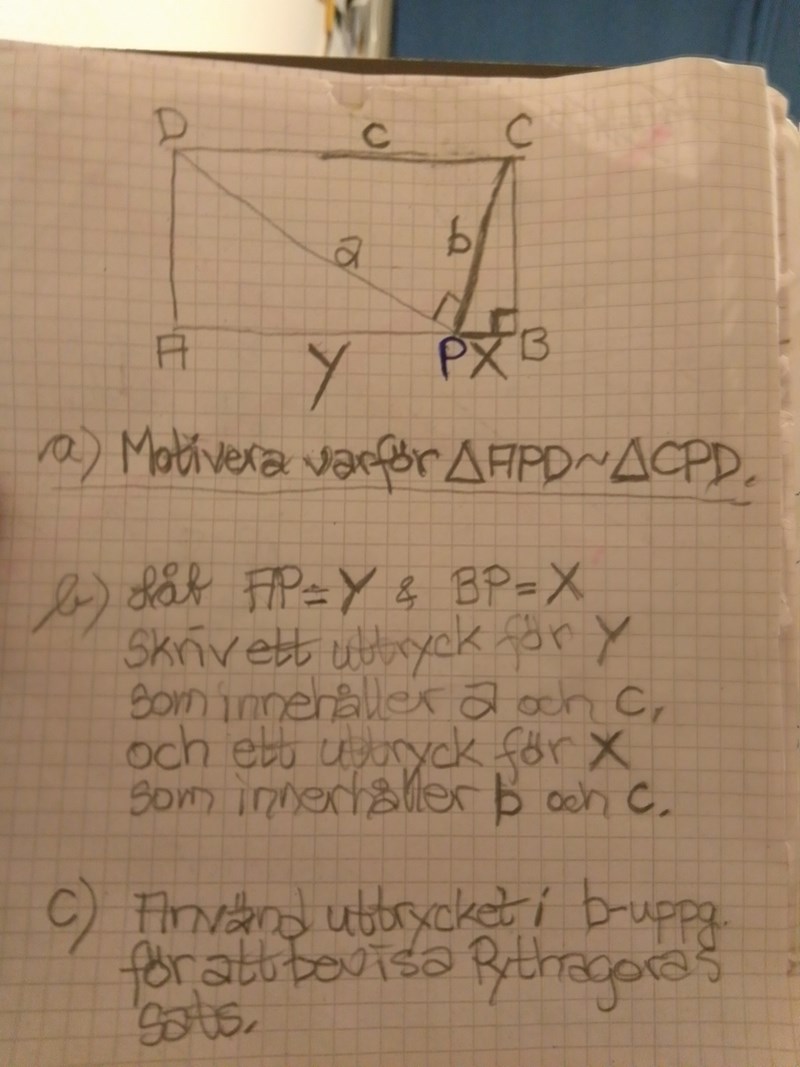 Hoppas bilden går att tolka, jag har inte tillgång till matteboken just nu!
Hoppas bilden går att tolka, jag har inte tillgång till matteboken just nu!
Samma storlek har de inte. Du ska visa att de är likformiga.
 I b-uppgiften förstår jag inte hur jag ska kunna skriva ett uttryck för y som innehåller c?
I b-uppgiften förstår jag inte hur jag ska kunna skriva ett uttryck för y som innehåller c?
Henrik skrev:
I b-uppgiften förstår jag inte hur jag ska kunna skriva ett uttryck för y som innehåller c?
Om du kollar på trianglarna i figuren? Vilka sidor är gemensamma? Om du skriver formler och uttryck för alla, finns det ngt sätt de kan kombineras?
De enda gemensamma sidorna jag kan se är att den längre katetern i den övre triangeln (a) är densamma som hypotenusan i den undre triangeln (a). Ser även att y=c-x, men sen kommer jag inte längre!
I figuren är DC parallell med AB.
Med hjälp av Bubos ledtråd i svar #6 så kan du konstatera att vinklarna u i bilden är lika stora. (Läs gärna om inre alternatvinklar här.)
Det betyder att de båda trianglarna APD och CPD har lika stora vinklar, vilket i sin tur innebär att de ör likformiga.
Fråga gärna om något av det känns oklart.

mrpotatohead skrev:Henrik skrev:
I b-uppgiften förstår jag inte hur jag ska kunna skriva ett uttryck för y som innehåller c? Den enda gemensamma sidan jag hittar är a.
Om du kollar på trianglarna i figuren? Vilka sidor är gemensamma? Om du skriver formler och uttryck för alla, finns det ngt sätt de kan kombineras?
Henrik skrev:
I b-uppgiften förstår jag inte hur jag ska kunna skriva ett uttryck för y som innehåller c? Den enda gemensamma sidan jag hittar är a.
Du kan utnyttja att även triangeln CBP är likformig med de två trianglar som nämns i a-uppgiften.
Ser du varför det är så?
Mha Likformighet kommer jag i b-uppgiften fram till att x=b2÷c, och att y=a2÷c.
Men hur ska jag använda dessa uttryck för att i c-uppgiften bevisa Pythagoras sats?
Henrik skrev:Mha Likformighet kommer jag i b-uppgiften fram till att x=b2÷c, och att y=a2÷c.
Men hur ska jag använda dessa uttryck för att i c-uppgiften bevisa Pythagoras sats?
Tips: I figuren ser du att c = x+y





