Gitterekvation

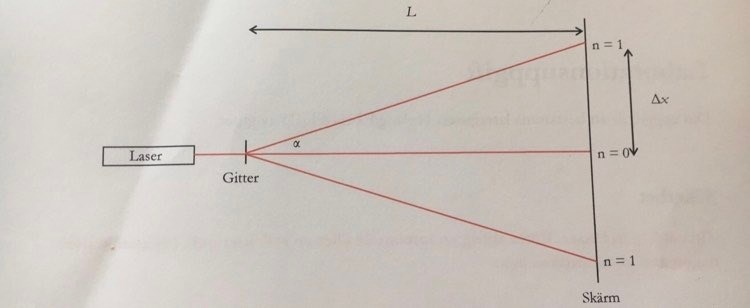
Tänker jag rätt med beräkningen? det men vinkeln undrar jag över. För jag har beräknat mha pythagoras sats alla tre sidor.
Du har beräknat värdet för , men själva vinkeln är ungefär 3.9° till första ordningen.
Jag tycker alltså att du antingen ska skriva ut vad vinkeln är, eller bara notera att
Edit: Du kanske har räknat i radianer? Då ser det ok ut eftersom för små vinklar. Men tycker ändå du ska redovisa hur du beräknat vinklarna.
använt miniräknaren och den var på degrees
Kan det inte vara grader? har beräknat vinklarna med hjälp av pythagoras sats. Kan lägga in en bild
EDIT: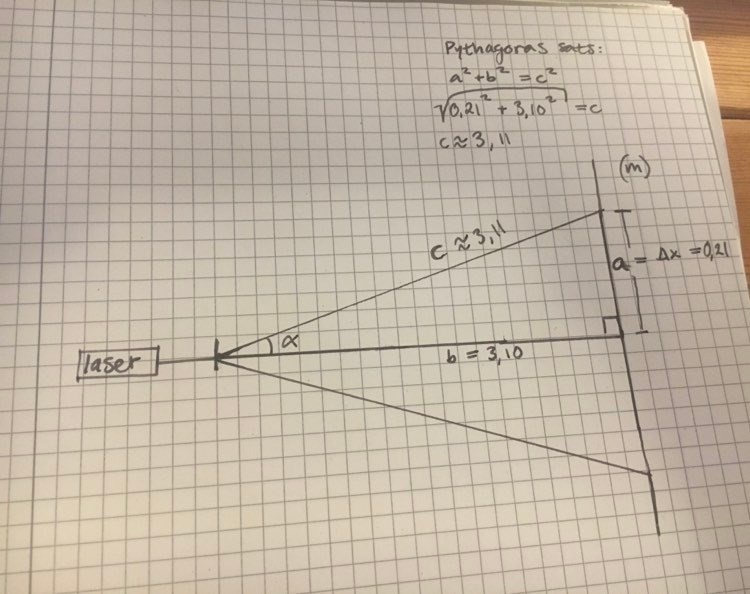
Du har skrivit sin 0.068.
Det betyder sinusvärdet för en vinkel som är 0.068
Sinus för 0.068 radianer är ungefär 0.068
Sinus för 0.068 grader är ungefär 0.00107
vad är det korrekta att skriva, jag måste skrivit fel.
sin v är a/c,
a är 0,21 m och
c är 3,11
Är det sin(0,21/3,11) isåfall?
Det blir då 0,0011785179, litet tal för att räkna med tycker jag, då vinkeln blir 0,0675 grader?
Vinkeln blir INTE 0.0675°.
Sinusfunktionen är en funktion.
Den tar ett argument (en vinkel) och ger dig ett tal.
Talet är förhållandet mellan motstående katet och hypotenusan i en rätvinklig triangel. I din bild blir det så här:
Vi stoppar alltså in i din vinkel och funktionen ger oss då förhållandet mellan och
Eftersom förhållandet mellan motstående katet och hypotenusan är ungefär betyder det att
Om man vill kan man räkna ut vinkeln från ekvationen. I grader blir vinkeln
Prova att slå på miniräknaren så får du talet , dvs förhållandet mellan motstående katet och hypotenusan i din rätvinkliga triangel.
jag ska beräkna våglängd mha gitterekvationen. Jag behöver veta vilka värden jag ska skriva in i miniräknaren, stämmer det att jag ska skriva in 1/100000*sin(a/c)= n*lambda?
sin⁻¹(0,21/3,10)= 3,9 grader
men det är inte arcsin jag ska ha, utanjag måste väl skriva sin(a/c) för att ekvationen ska stämma?
Nej är inte en vinkel, du får alltså inte skriva
Däremot får du använda att du vet att , så här
För blir det (lös ut )
Du kan också skriva så här:
okej, då förstår jag.
sin⁻¹(0,21/3,11) då får jag 3,872 grader om jag avrundar, hur får du 3,875?
kan jag skriva v= sin⁻¹(a/c)?
Jag räknade med fler (typ alla siffrorna), du har avrundat ganska hårt.
Personligen lär jag mina studenter att alltid skriva
för att inte blanda ihop det med
Men jag förstår att du vill skriva eftersom det kanske står så på din miniräknare. Det viktiga är att du själv och den som läser dina beräkningar VET vad du menar.
ja, oj, då förstår jag!
Ska skriva arcsin istället.
Jaha okej, men då avrundar jag lite mer korrekt. Tack för hjälpen.
jag förstår ändå inte hur du får 3,87179202 till 3,875?
ja, okej du avrundade redan vid hypotenusan.
En annan fråga, våglängden för 100 linjer/mm ska väl vara samma för alla ordningar? Jag fick att det fanns 4 ordningar åt vänster och höger, de alla ska ha samma våglängd väl?
OliviaH skrev:En annan fråga, våglängden för 100 linjer/mm ska väl vara samma för alla ordningar? Jag fick att det fanns 4 ordningar åt vänster och höger, de alla ska ha samma våglängd väl?
Ja, du kommer få ungefär samma våglängd, beroende lite på hur exakta dina mätningar var och hur hårt du avrundar. (Förutsatt att ni använde samma laserpekare hela tiden)
Första ordningen var andra ordningen ger
jag får 680 nm och 670 nm. Men då vet jag att det ska vara samma våglängd, det är ju mina avrundningar som gör den stora skillnaden.
OliviaH skrev:jag får 680 nm och 670 nm. Men då vet jag att det ska vara samma våglängd, det är ju mina avrundningar som gör den stora skillnaden.
... och då vet du att du har avrundat för mycket.
jag får 675 och 671 om jag avrundar i slutet ändå såg jag nu
Ja, det stämmer.
Avstånden 84cm, 42cm och 310cm skulle ju kunna vara någon millimeter fel, och då kan beräknad våglängd bli någon nanometer fel.


