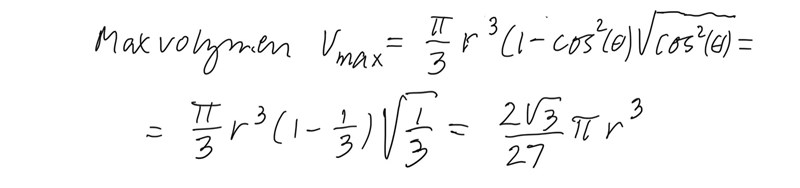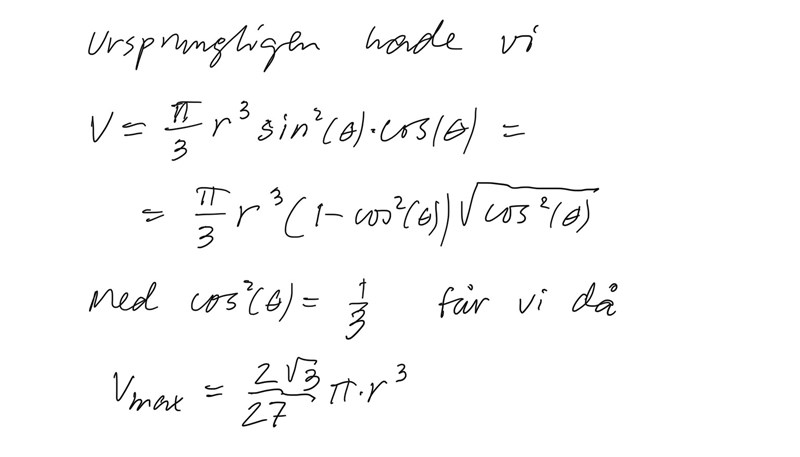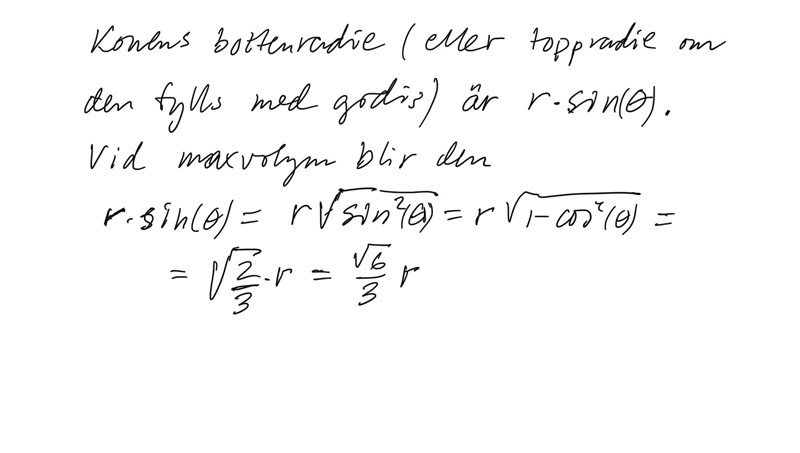Godisstruten - omfångsrika problem
Hej, jag har en fråga jag skulle behöva hjälp med.
Frågan lyder:
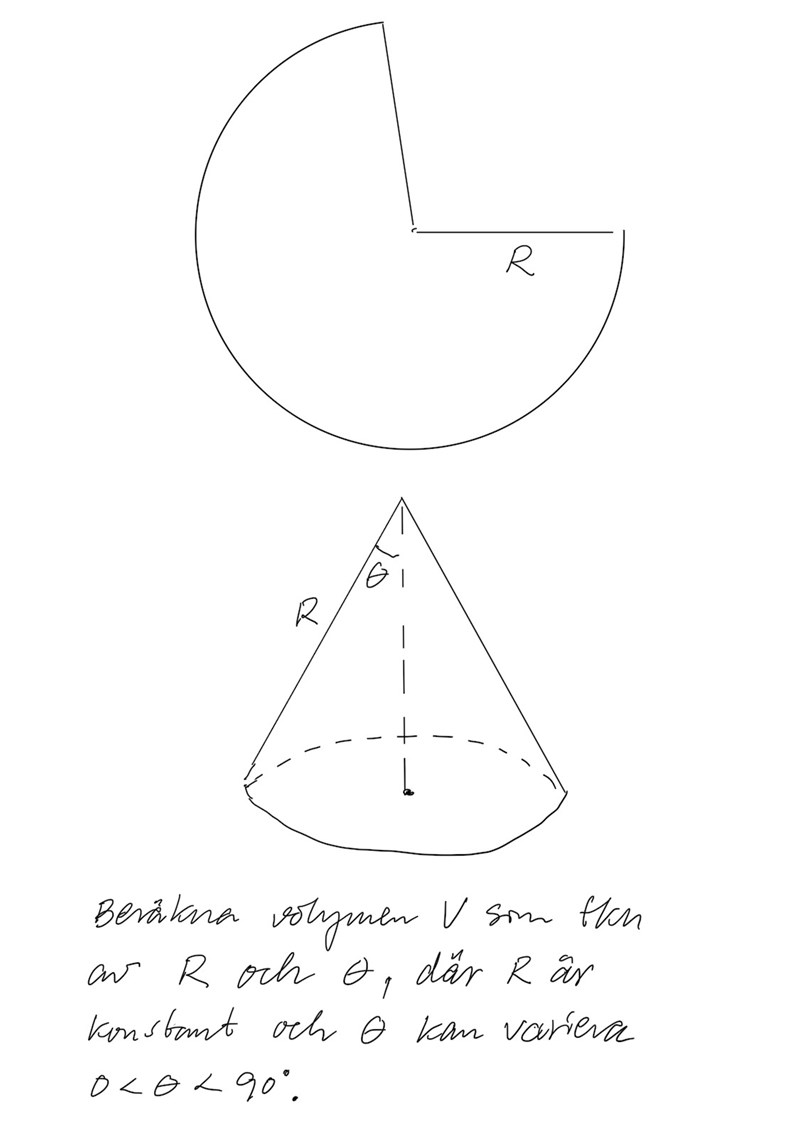
Emelie ska sälja hemlagat godis på en marknad. Hon har fått en bunt papper som är cirkelformade och undrar hur hon ska klippa till dessa för att struten som hon ska ha godiset i ska få så stor volym som möjligt.
Ur ett papper med formeln av en cirkelskiva med radien r klipper hon först ut en cirkelsektor. Därefter sammanbinder hon snittytorna så att det bildas en kon.
Hur stor cirkelsektor ska hon klippa bort från cirkelskivan för att få den maximala volymen?
Jag har kollat upp vilken formel som bör användas i syfte att lösa denna uppgift vilken jag antar bör vara båglängden = (v/360grader)*2r*pi
Att lösa ut den maximala volymen kan jag dessutom göra genom att ställa upp en funktion för konens volym som funktion av konens höjd och sedan derivera den och lägga derivatan är lika med noll för att ta reda på maxpunkten och därefter ta reda på maxvolymen. Maxvolymen blev (2*pi*r^2)/9*3^0.5
Men jag ser inte ett sätt för att sedan kunna gå vidare och lösa ut hur stor cirkelsektorn bör vara, skulle uppskatta lite hjälp.
Okej, tack så mycket, så volymen av en kon ges av formeln: (pi*r^2*h)/3.
r i formeln är R.
Om vi skriver vinkeln som v.
Antagligen beror höjden på vinkeln v. Men cos får jag fram att cos (v) = h/R. Byter jag ut h får jag R*cos(v).
Insatt i volym formeln får jag:
(pi*R^2*R*cos(v))/3
Är detta rätt? Och hur går jag vidare för att kunna ta ut vinkeln från funktionen?
Jag förstår inte hur du ställde upp funktionen, försöker komma på hur den blev som den blev men förstår inte, skulle du kunna förklara hur den blev som den blev. Sen att derivera den är enkelt, men vad får jag fram när jag sätter derivatan lika med noll, vinkeln eller?
Okej, tack så mycket för förklaringen, den var jättetydlig, men hur skulle man utifrån detta uttryck för volymen ta reda på den maximala volymen för konen? Är det möjligt? För jag skulle anta att man deriverar uttrycket likt du har gjort och sätter derivatan lika med noll för att få ut maximal volym, dock verkar man inte få ut den maximala volymen utifrån detta i och med att man får ut vinkel, så min fråga blir huruvida det går att ta reda på den maximala volymen utifrån samma uttryck och om inte hur skulle man då kunna göra det?
Förlåt om jag frågar mycket men var kom detta uttryck ifrån? Är det derivatan av ett annat uttryck?
Jaha, då förstår jag, tack så mycket. Men skulle det möjligtvis kunna finnas ett sätt att ta reda på vilken radie det är som ger den maximala volymen?
Jag förstår vad du menar, men tänker mer i form av att få fram ett specifikt svar på radien, men det kanske iförsej inte är möjligt i och med att inga värden är angivna i frågan, eller?
De cirkelformade pappersarken hade ju en viss storlek som hon i alla fall inte kunde göra större. Volymen ändras förstås med längdskalan i kubik.
Tack så mycket för hjälpen, det uppskattas.
Hej, jag undrar hur bågen blev 2pi*r*sin(x). Det vill säga varför blev vinkeln 2*pi*sin(x)? Hur kom sin(x) in i allt och varför inte cos(x)?
Omkretsen på strutens bottenyta är 2πr*sin(θ), eftersom motsvarande radie är r*sin(θ). Båglängden på det avklippta cirkulära papperet är lika med strutens omkrets dvs 2πr*sin(θ). Den kvarvarande vinkeln efter urklippet är båglängden dividerat med radien, dvs 2π*sin(θ).
Hur kan vinkeln vara båglängden dividerat med radien ?
anonym000 skrev:Hur kan vinkeln vara båglängden dividerat med radien ?
Det är den, om man mäter vinkeln i radianer.
Smaragdalena skrev:anonym000 skrev:Hur kan vinkeln vara båglängden dividerat med radien ?
Det är den, om man mäter vinkeln i radianer.
Kan du förklara lite mer ?