Gradienter

Gradienten har olika längd beroende på hur mycket funktionen ändras. Om man skalärmultiplicerar gradienten med en riktningsvektor $\nabla f \cdot \hat{v}$ får man hur mycket funktionen ändras i just den riktningen.

På en nivåyta $f(x,y,z)=C$ är funktionen konstant $f=C$ och ändras inte alls! Alltså måste gradienten vara vinkelrät mot nivåytan eftersom den pekar i den riktning $f$ ändras mest. Vilket INTE kan vara utmed ytan, eftersom den är konstant $C$ där. Är du med?

TLDR: nej jag förstår fortfarande inte

Skalärmultiplicerar vi med en riktningsvektor just för att gradienten har längd 1 och resten... Asså va? Gradienten anger väl riktning, riktningsvektorn ger dess storlek? Känner mig hyper-förvirrad. Det make:ar dock mer sense att RIKTNINGSvektorn anger riktningen medan gradienten kanske anger storleken. Men jag läste i en sats att grad f(a,b) är en NORMALvektor... ahh vänta... inte NORMerad = $\ne NORMal$... tror jag blandade ihop de kanske

Men kolla, jag hänger inte med på den andra heller. Jag hänger med att funktionen är konstant men kolla om vi är i rummet, det nivåytan är är väl att vi tar en "strip" på den höjden av den kroppen. På den här "stripen" så kan en vektor riktas i vilken riktning som helst? Asså nu när jag tänker på det. Liksom tänk om vi tar en strip/del av en mantelarea för någon kropp... hur i helskottan ska man veta om det är en del som är brant eller inte brant om man bara har den delen och inte resten av kroppen? För man kunde väl se det som höjdkurvor på en karta typ.

Ja, gradienten bildar normal (är vinkelrät) till nivåytan. Men den är inte NORMerad.  Tvärtom har den olika längd.

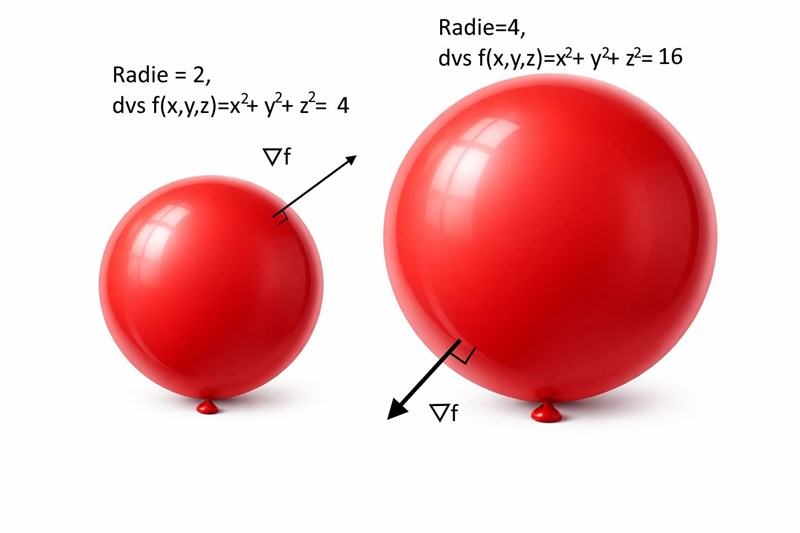
Här är två ballonger som kan få illustrera två nivåytor till funktionen $f(x,y,z)=x^2+y^2+z^2$. Det är alltså två sfäriska ytor.

Gradienten är $\nabla f = (2x,2y,2z)$

I vilken punkt du än räknar på den röda ytan kommer den ge en vektor som är vinkelrät mot den röda ballongytan. Gradienten ger dig information om funktionens lokala uppförande runt en punkt. Den kan ju ge olika värden och olika riktningar i olika punkter.

Men gradienten pekar alltid åt det håll funktionen växer mest. Och för en ballong blir det vinkelrätt mot ballongytan, radiellt utåt. 

Okej hänger hyfsat med... så båda dessa ballonger har samma gradient. Det jag tycker är intressant är hur man kan veta i vilken riktning en funktion växer mest. Funktionen växer just mest radiellt utåt i detta fall... ingen annan riktning... just VINKELRÄT ska vara den snabbaste riktningen funktionen växer. Vinkelrät utåt dessutom