Graf - integral - flera val

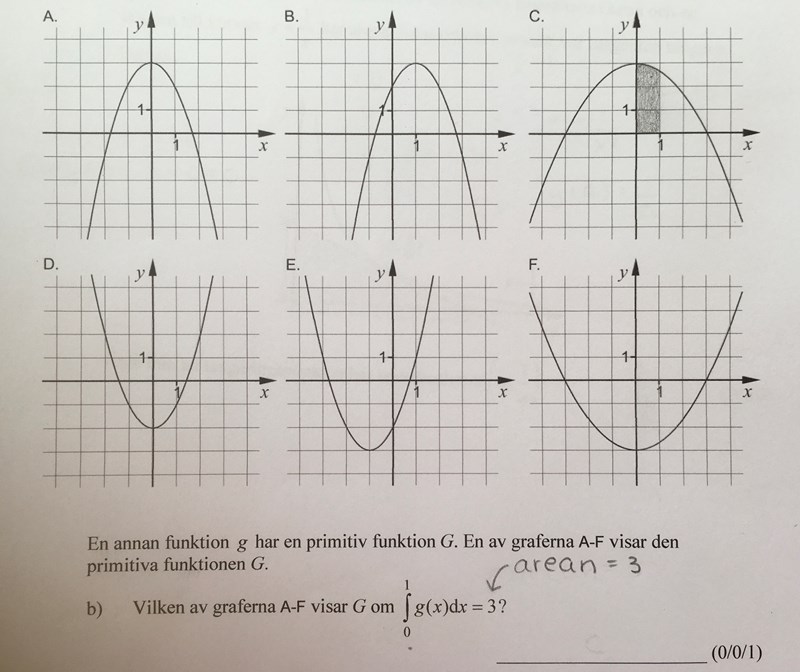
Det stämmer att integralen visar arean under en graf, men vilken funktion är det som visas i figurerna?

Jo alltså jag förstår ju att det är g(x) som är funktionen och att det som visas i graferna redan är den primitiva funktionen G men jag vet inte riktigt vad 3an liksom "symboliserar". Att lutningen mellan 1 & 0 ska vara =3? 

Eller vänta lite!  G(1) - G(0) ska bli = 3 dvs grafens y-värden i punkterna - varandra ska bli = 3

Stämmer mitt resonemang där? 

katt-katten skrev:

Eller vänta lite!  G(1) - G(0) ska bli = 3 dvs grafens y-värden i punkterna - varandra ska bli = 3

Stämmer mitt resonemang där? 

Ja. Så vilken figur passar bäst in på det?

Ah då blir det ju figur E som det ska bli! Tack för hjälpen!

Kan man då säga att en integral betyder 

1. Arean under grafen då funktionen är f(x) 

2. Skillnad i funktionsvärden då funktionen är F(x) ( = $\Delta h$ (där h är höjden/y-värdet) i en F(x) funktion) 

katt-katten skrev:

Kan man då säga att en integral betyder 

1. Arean under grafen då funktionen är f(x) 

Ja, den definition av integral som du lär dig är "arean under grafen". Problem med denna definition kommer exempelvis som här:

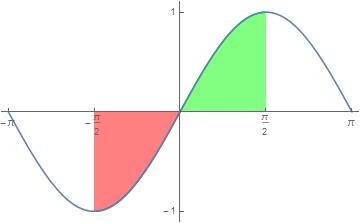
Om du bara tittar på bilden så ser du att röda fältet plus gröna fältet är tydligt en area. Om du däremot beräknar integralen:

$\displaystyle \int_{-\pi/2}^{\pi/2}sin\left(x\right)dx=\left[cos(x)\right]_{-\pi/2}^{\pi/2}=0$

Alltså är integralen lika med noll trots att du ser en tydlig area. Det är därför det är bättre att kalla denna definition av integralen för den teckenkänsliga arean under grafen (Engelska: signed area under the curve). 

2. Skillnad i funktionsvärden då funktionen är F(x) ( = $\Delta h$ (där h är höjden/y-värdet) i en F(x) funktion) 

Ja, precis. En integral definieras som:

$\displaystyle \int_{a}^{b} f\left(x\right)dx=F\left(b\right)-F\left(a\right)$

Där vi har det du kallar $\mathrm{\Delta }h=F\left(b\right)-F\left(a\right)$.