Grafen visar funktionen. Bestäm Amplitud, period och förskjutning.

Exponent 4 (2013), uppgift 1081

I denna uppgift så får vi en graf till funktionen $f\left(x\right)=A\sin k(x+B°)$

Där vi ska bestämma A, k och B. 

Graf b) ser ut såhär:

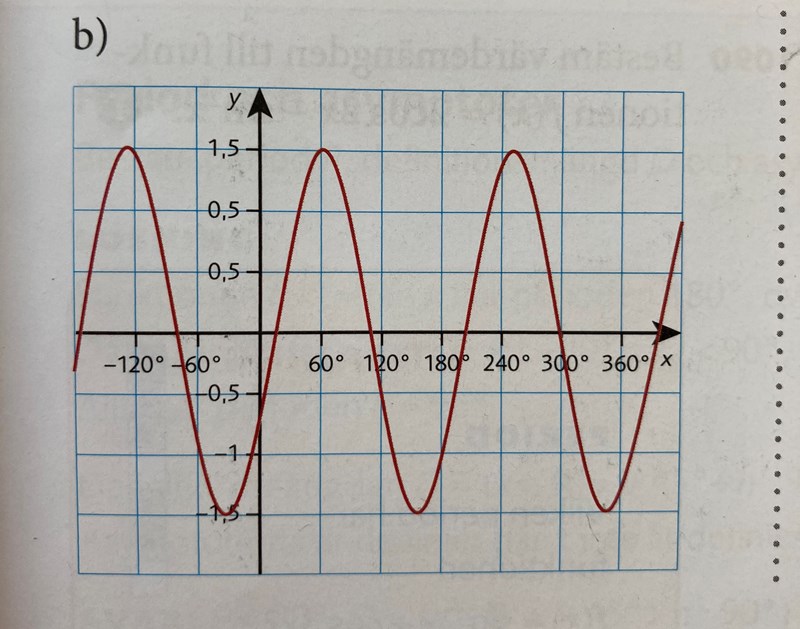
Efter en titt på grafen kan jag ganska snabbt bestämma A och k där A=1,5 och k=2 och nu vet vi såhär mycket om funktionen; $f\left(x\right)=1,5\sin 2(x+B°)$

Därefter vill jag ta reda på förskjutningen, dvs värdet på B. För att ta reda på B vill jag gärna hitta en godtycklig punkt för att kunna stoppa in ett värde på x och y för att få ut B. Jag väljer punkten (0;-0,75) och får ekvationen

$1,5\sin 2(0+B°)=-0,75$

Löser vi den får vi $B=-15°+n\times 180°$ och då ser vi att vi har en förskjutning på grafen med 15 grader till höger. Vilket stämmer överens med facit.

Då undrar jag om jag har tänkt rätt när jag har löst uppgiften? Det som gör mig lite osäker är att det är en ren uppskattning från min sida att där x=0 ger y-värdet -0,75 som ger mig punkten (0;-0,75)  och som hjälper mig att ta reda på förskjutningen av grafen. Finns det andra sätt att ta reda på förskjutningen?

Nu kommer vi till graf c) som jag inte vet hur jag tar reda på förskjutningen hos.

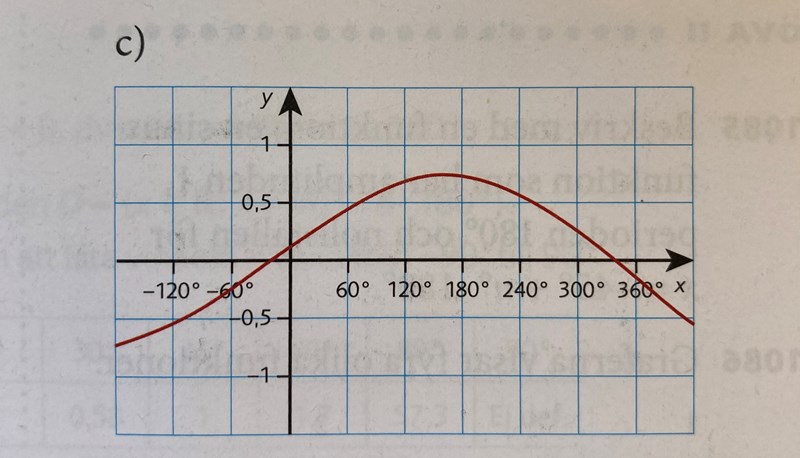
Tar man en titt på grafen kan man ganska snabbt bestämma A och k, A=0,75 och k=0,5, men vad ska jag börja titta på för att kunna få fram förskjutningen här? Jag ser ingen lämplig punkt för att använda mig av samma strategi som tidigare graf. Facit säger: $f\left(x\right)=0,75\sin 0,5(x+20°)$

Tacksam för lite tips här. 

Mvh!