Grafer
Hej! Jag behöver lite hjälp med följande uppgift:
- Grafen till f(x) = x^2+ 2x + 3 har en tangent med lutningen - 2 och en annan tangent med lutningen 4. Bestäm koordinaterna för den punkt där de bada tangenterna skär varandra.
Jag vet inte ritkogt hur jag ska börja men jag antar att man behöver derivera funktionen vilket blir y’=2x-2
Men sen vet jag inte hur jag ska göra.
Med derivatan kan du ta reda på k-värdet i båda tangenterna.
Sedan behöver du deras m-värdet.
Tillsist sätter du ekvationerna lika varandra för att ta reda på skärningspunkten.
mrpotatohead skrev:Med derivatan kan du ta reda på k-värdet i båda tangenterna.
Sedan behöver du deras m-värdet.
Tillsist sätter du ekvationerna lika varandra för att ta reda på skärningspunkten.
Juste!
Jag har räknat ut att den ena tangenten med lutningen -2 har x-värdet -2 och den andra har x-värdet 4. Men om jag inte har någon punkt angiven hur kan jag ta reda på resten av ekvationen
Börja med att rita upp grafen till f(x) och skissa in de båda tangenterna, så att du ser på ett ungefär var de skär varandra. Det gör att du kan märka om din lösning blir fel, och det kan vara väldigt bra att veta...
Smaragdalena skrev:Börja med att rita upp grafen till f(x) och skissa in de båda tangenterna, så att du ser på ett ungefär var de skär varandra. Det gör att du kan märka om din lösning blir fel, och det kan vara väldigt bra att veta...
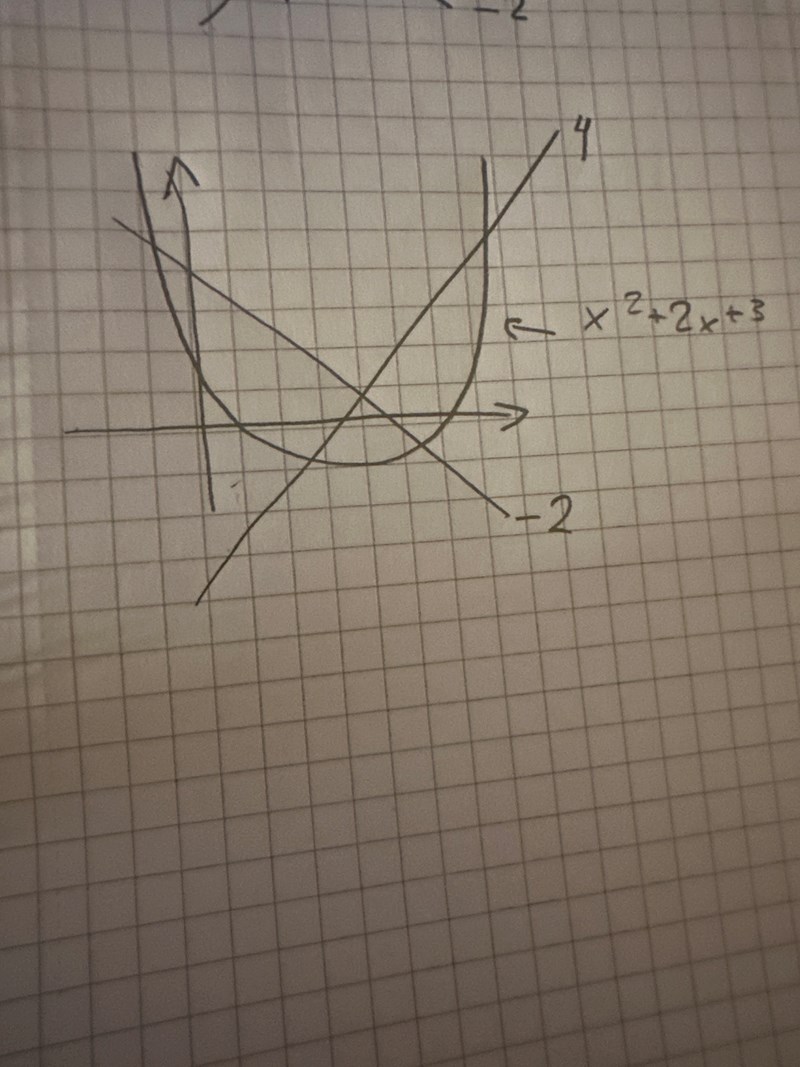
Typ såhär
De där linjerna är inga tangenter, och du bör vara lite mer petig med lutningen om du skall kunna ha någon nytta av bilden.
Som Smaragalena skriver, en korrekt bild är av stor vikt! (Rätt bild och uppgiften är till 50% klar. Vad du ritat gör uppgiften 30x svårare än vad den är…) Kan f(x) ens skära x-axeln?
Trinity2 skrev:Som Smaragalena skriver, en korrekt bild är av stor vikt! (Rätt bild och uppgiften är till 50% klar. Vad du ritat gör uppgiften 30x svårare än vad den är…) Kan f(x) ens skära x-axeln?
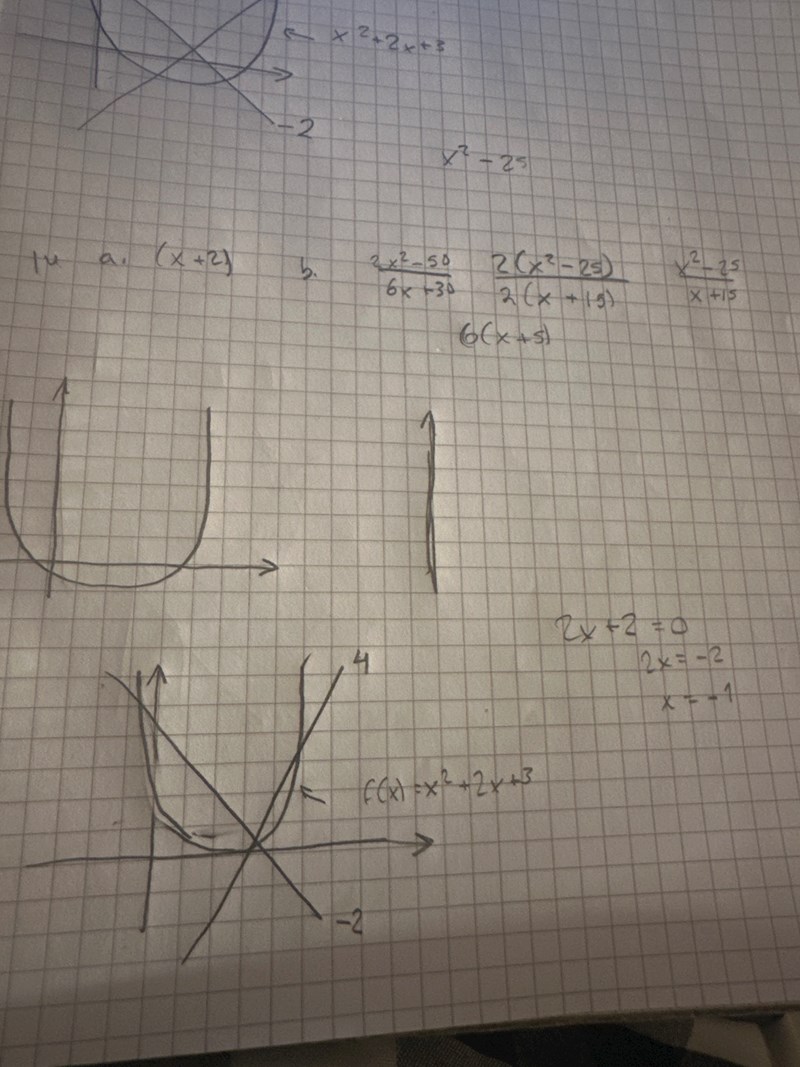
Jag hoppas detta är bättre 🥹
Du har rätt med att grafen inte har några nollställen och därför bör den inte överskrida x-axeln. Men hur går jag vidare nu?
Sök upp vad tangent betyder och gör ett nytt försök😃
mrpotatohead skrev:Sök upp vad tangent betyder och gör ett nytt försök😃
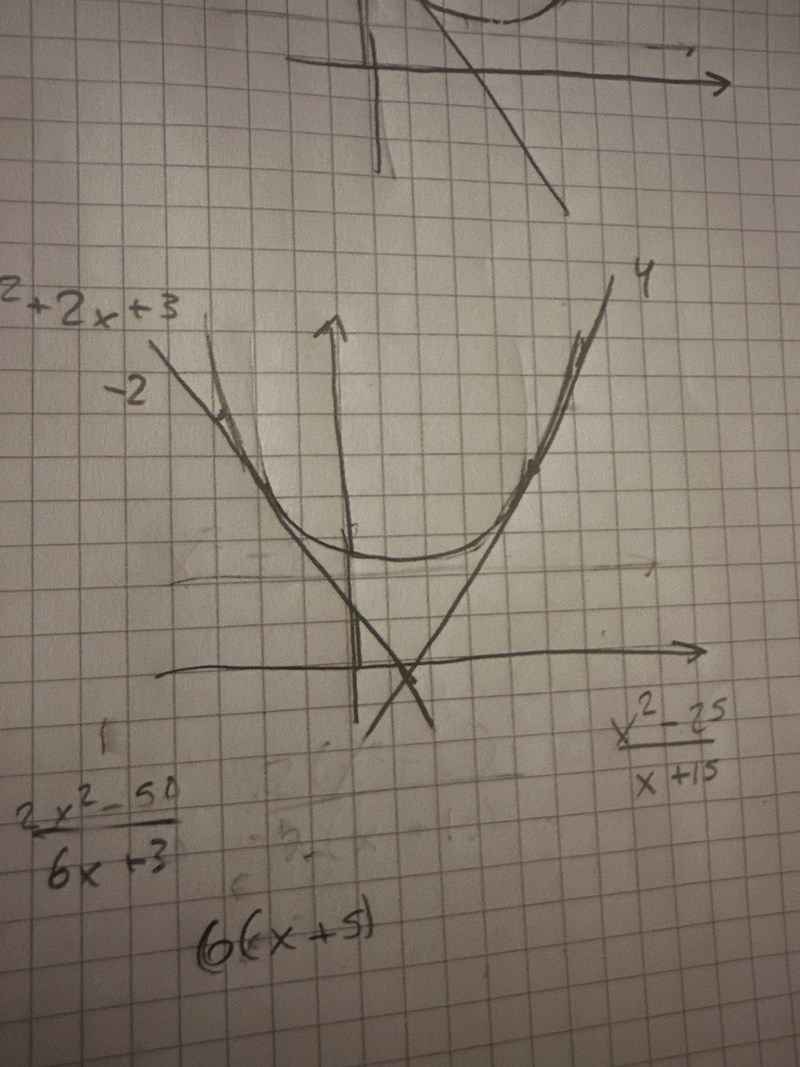
Jag ber om ursäkt jag kopplade verkligen inte 🥲
Såhär kanske?
shorjs skrev:mrpotatohead skrev:Sök upp vad tangent betyder och gör ett nytt försök😃
Jag ber om ursäkt jag kopplade verkligen inte 🥲
Såhär kanske? Det ser inte så skalenligt men tangenterna är iallafall bättre
Det ser bättre ut, dock (märkte nu att jag läste fel i frågan första gången och trodde det stod punkterna -2 och 4 inte lutningarna.. hehe) borde den växande vara dubbelt så brant som den avtagande. Du kan väl testa en sista gång, men jag tycker inte det är så noga. Nu förstår du i alla fall vad du ska lösa!
mrpotatohead skrev:Det ser bättre ut, dock (märkte nu att jag läste fel i frågan första gången och trodde det stod punkterna -2 och 4 inte lutningarna.. hehe) borde den växande vara dubbelt så brant som den avtagande. Du kan väl testa en sista gång, men jag tycker inte det är så noga. Nu förstår du i alla fall vad du ska lösa!
Jag återkommer imorgon! Är för trött för att hålla ögonen öppna just nu 🥲
Nyckeln till framgång inom matematik (nåja...) är en bra bild.
Du kanske ser att det är en parabel men om du inte gör det är det en funktionstabell som gäller
Tag x = -4, -3, ..., 4, 5 och beräkna y värdet.
Sedan plottar du in punkterna i ett koordinat system och skissar grafen.
Sedan är det dags att fundera på vad en tangent är. Googla om du är osäker och därefter börja fundera på var en tangent till kurvan kan ha lutningen -2 och +4 (det är två olika tangenter). Detta ger en uppskattning och en bild över situationen.
Återkom sedan så fortsätter vi därifrån.



