Gränserna.

För ett klot gäller att radien går från 0 till r, fi går från 0 till 2 pi (tänk hela varvet runt ekvatorn) och theta går från 0 till pi (tänk dig från sydpolen till nordpolen, med lämpligt vald riktning för 0).

Smaragdalena skrev:

För ett klot gäller att radien går från 0 till r, fi går från 0 till 2 pi (tänk hela varvet runt ekvatorn) och theta går från 0 till pi (tänk dig från sydpolen till nordpolen, med lämpligt vald riktning för 0).

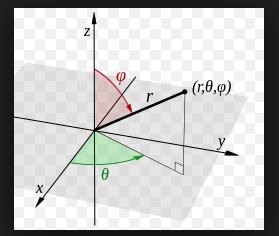
OK, för nu tänker jag att jag ska lära mig att rita. (när jag googlar kordinatsystem för cylinder och klot så fick jag att det ser ut såhär (båda två) är det sant?)

Då går radien från origo till r (r i det här fallet är 2), 
och det är ett klot så den måste bli rund (och därför 0 till 2pi) asså fi... Fråga1: varför är det just fi som går runt (asså tänker nu på bilden) går runt ett varv och inte theta?
thetha går från 0 till pi, Fråga2: Varför går den bara ett halvt varv?

alltså försöker verkligen med hela mitt hjärta se hur det här ser ut, men blir svårt när det är R3

Hej heymel,

Av tradition brukar vi i Sverige (iaf på de flesta tekniska högskolor och universitet) använda $\theta$ som vinkeln FRÅN z-axeln till punkten (se figur). Man låter då $\theta$ löpa från $0$ till $\pi$. Vinkeln FRÅN x-axeln till punkten (se figur) kallas $\varphi$ Den löper då från $0$ till $2\pi$.

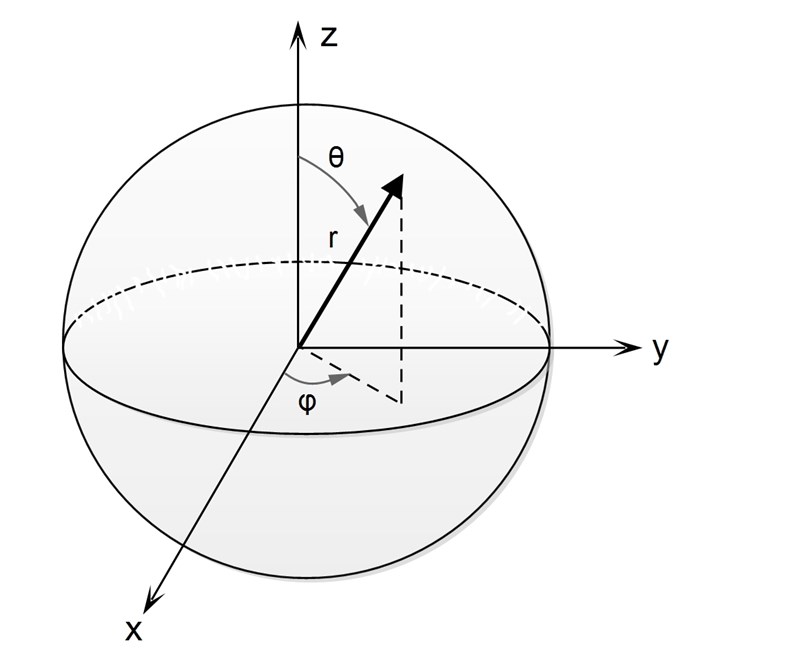Sfäriska koordinater $(r,\theta, \varphi)$

Detta är också den vanligaste definitionen inom fysik.  Det går självklart bra att byta namn på vinklarna (dvs $\theta$ byts ut mot $\varphi$ och vice versa), och det är det vanligt inom äldre matematisk litteratur. Du kan också byta intervall, men för att inte göra slarvfel är det bäst att

• Använda det din kurslitteratur och din föreläsare använder
• Använda samma intervall och uppsättning varje gång
• Känna till uppräkningsordningen, i ovanstående definition är ordningen $(r,\theta, \varphi)$

En av vinklarna måste gå hela varvet runt, den andra vinkeln går bara halva varvet runt, annars adresserar du samma punkter i klotet flera gånger, det får du inte göra.

Guggle skrev:

Hej heymel,

Av tradition brukar vi i Sverige använda $\theta$ som vinkeln FRÅN z-axeln till punkten (se figur). Man låter då $\theta$ löpa från $0$ till $\pi$. Vinkeln FRÅN x-axeln till punkten (se figur) kallas $\varphi$ Den löper då från $0$ till $2\pi$.

Sfäriska koordinater $(r,\theta, \varphi)$

 Det går självklart bra att byta namn på vinklarna (dvs $\theta$ byts ut mot $\varphi$ och vice versa. Det är vanligast inom äldre matematisk litteratur. Du kan också byta intervall, men för att inte göra slarvfel är det bäst att

• Använda det din kurslitteratur och din föreläsare använder
• Använda samma intervall och uppsättning varje gång
• Känna till uppräkningsordningen, i ovanstående definition är ordningen $(r,\theta, \varphi)$

En av vinklarna måste gå hela varvet runt, den andra vinkeln går bara halva varvet runt, annars adresserar du samma punkter i klotet flera gånger, det får du inte göra.

 Ah okej, och använda samma uppräkningsordning $(r,\theta, \varphi)$ då blir det att man först integrerar phi? sedan theta och sist r?

heymel skrev:

 Ah okej, och använda samma uppräkningsordning $(r,\theta, \varphi)$ då blir det att man först integrerar phi? sedan theta och sist r?

Nej, du får oftast integrera i vilken ordning du vill.  Uppräkningsordningen avgör basvektorernas inbördes ordning. På samma sätt som det  kartesiska koordinatsystemet håller ordningen $(x,y,z)$. Det är viktig att hålla reda på av flera skäl, t.ex. när du transformerar dina koordinater. Det är också viktigt att skalfaktorerna hamnar rätt när du ställer upp saker som gradienten, divergensen eller rotationen, exempel:

$\nabla f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial \theta}\hat{\theta}+\frac{1}{r\sin(\theta)}\frac{\partial f}{\partial \varphi}\hat{\varphi}$

Guggle skrev:

heymel skrev:

 Ah okej, och använda samma uppräkningsordning $(r,\theta, \varphi)$ då blir det att man först integrerar phi? sedan theta och sist r?

Nej, du får oftast integrera i vilken ordning du vill.  Uppräkningsordningen avgör basvektorernas inbördes ordning. På samma sätt som det  kartesiska koordinatsystemet håller ordningen $(x,y,z)$. Det är viktig att hålla reda på av flera skäl, t.ex. när du transformerar dina koordinater. Det är också viktigt att skalfaktorerna hamnar rätt när du ställer upp saker som gradienten, divergensen eller rotationen, exempel:

$\nabla f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial \theta}\hat{\theta}+\frac{1}{r\sin(\theta)}\frac{\partial f}{\partial \varphi}\hat{\varphi}$

 oki. Tror jag är med. ska kolla på fler uppgifter :)