4
svar
80
visningar
ugglebulle är nöjd med hjälpen
Gränsvärde
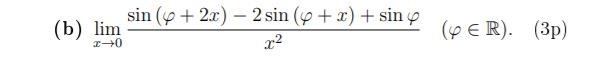
Hej vet inte hur jag ska lösa denna. (L'Hospital eller taylorutvecklings får inte användas)
Man ska utnyttja gränsvärdet av sin x/x x --->0 på något sätt men får inte till det.
Utveckla med additionssatser.
Gruppera.
Studera gränsvärden.
Hmmm, vi kan alltid prova med additions- och subtraktionsformeln för sinus:
Prova att bryta ut några olika gemensamma termer. Vad händer? :)
Tack så mycket :)
Varsågod! :)


