Gränsvärde blir fel

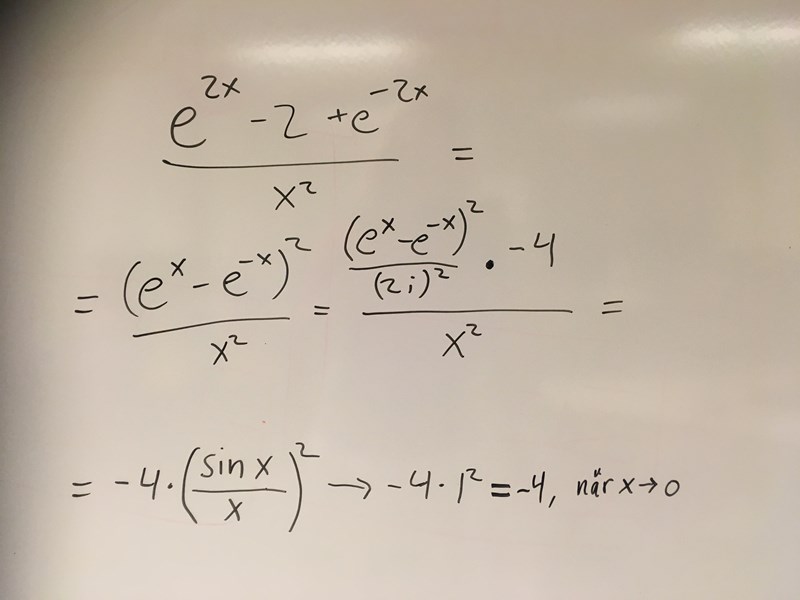
Du har inga i:n i exponenterna. Det blir således inte sin(x),utan sinh(x).

🤦‍♀️😅

Man kan också identifiera detta som andraderivatan:

$f''(0)=\lim_{x\to 0}\frac{f(x)-2\cdot f(0)+f(-x)}{x^2}$

för $f(x)=e^{2x}$

$f''(x)=2^2e^{2x}\Rightarrow$

$f''(0)=4\cdot e^0=4$

Hej,

Uttrycket kan skrivas $4\cdot(\frac{e^{x}-e^{-x}}{x-(-x)})^2$ där kvoten närmar sig derivatan till funktionen $e^x$ i punkten $x=0$ då $x$ närmar sig noll.

Man kan använda e^x = 1 + x + x²/2 + x³/6 + ... också.

Alla förslag här är flera kapitel fram i boken, det som var tänkt att göra var att förlänga med e^2x och sen få standardgränsvärde (e^x-1)/x fast med 2x och i kvadrat. Jag roade mig med att köra vidare på påbörjat spår. Får man göra såhär? Blev ju rätt svar iaf. 

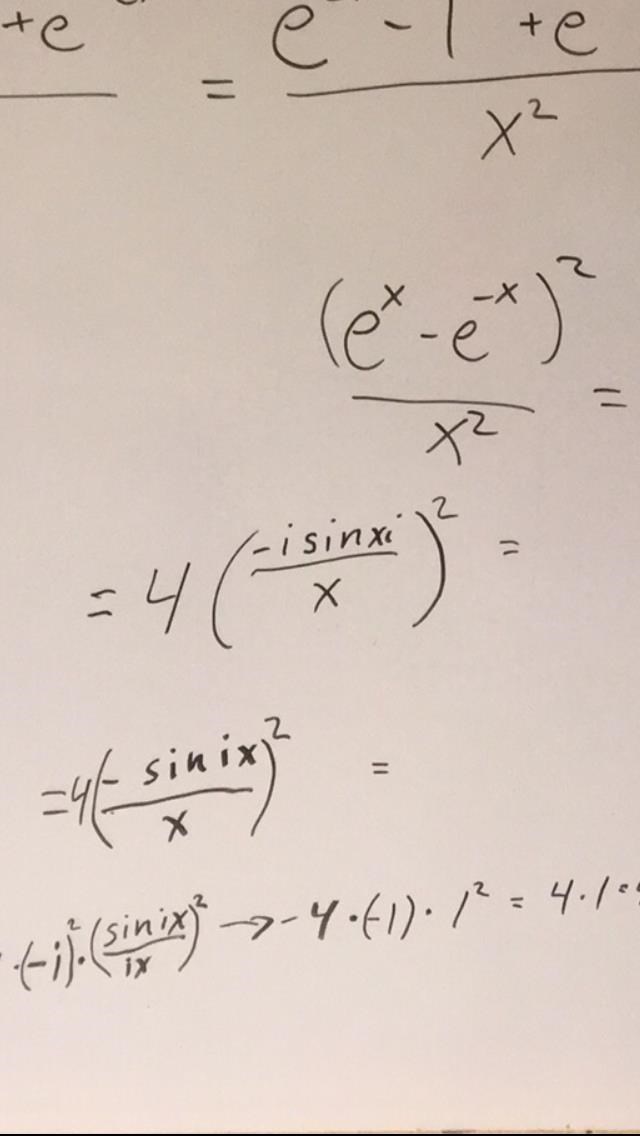
l'Hôpitals regel då?

Laguna skrev:

l'Hôpitals regel då?

Den används inte alls i kursen.

Micimacko skrev:

Laguna skrev:

l'Hôpitals regel då?

Den används inte alls i kursen.

Vad är det för kurs?

Tata41. Står förklarat på kurshemsidan varför den inte används, men inte tagit mig tid att tyda förklaringen.

Tata41

Enligt Google är det envariabelanalys på LiU.

Smaragdalena skrev:

Tata41

Enligt Google är det envariabelanalys på LiU.

Ja en av dem. Finns flera med samma namn men lite olika innehåll :)

Micimacko skrev:

Tata41. Står förklarat på kurshemsidan varför den inte används, men inte tagit mig tid att tyda förklaringen.

Hans Lundmark m. fl. anser att man inte ska använda l'Hospitals regel i TATA41/TATA42 utan att kunna härleda dess begränsningar och villkor tydligt under tentan (vilket någon aldrig gjort). Om du tar det gränsvärdet som är mest relevant för din uppgift:

$\underset{x\to 0}{\lim }\frac{\sin x}{x}$

Om du använder l'Hospitals regel för att lösa denna är det ett form av cirkelresonemang. Detta därför att du antar att du redan vet derivatan av sinus-funktionen men om vi tittar närmre på derivatans definition av den har vi:

$$\begin{gathered} \underset{h\to 0}{\lim }\frac{\sin (x+h)-\sin \left(x\right)}{h}=\underset{h\to 0}{\lim }\frac{{\displaystyle \sin \left(x\right)\cos \left(h\right)+\sin \left(h\right)\cos \left(x\right)-\sin \left(x\right)}}{{\displaystyle h}}= \\ =\cos \left(x\right)\left[\underset{h\to 0}{\lim }\frac{{\displaystyle \sin \left(h\right)}}{{\displaystyle h}}\right] \end{gathered}$$

Gränsvärdet du försöker lösa med l'Hospitals regel dyker upp i härledningen av derivatan. För referens kan läsas mer här:

Undervisnings-FAQ

Ebola skrev:

Micimacko skrev:

Tata41. Står förklarat på kurshemsidan varför den inte används, men inte tagit mig tid att tyda förklaringen.

Hans Lundmark m. fl. anser att man inte ska använda l'Hospitals regel i TATA41/TATA42 utan att kunna härleda dess begränsningar och villkor tydligt under tentan (vilket någon aldrig gjort). Om du tar det gränsvärdet som är mest relevant för din uppgift:

$\underset{x\to 0}{\lim }\frac{\sin x}{x}$

Om du använder l'Hospitals regel för att lösa denna är det ett form av cirkelresonemang. Detta därför att du antar att du redan vet derivatan av sinus-funktionen men om vi tittar närmre på derivatans definition av den har vi:

$$\begin{gathered} \underset{h\to 0}{\lim }\frac{\sin (x+h)-\sin \left(x\right)}{h}=\underset{h\to 0}{\lim }\frac{{\displaystyle \sin \left(x\right)\cos \left(h\right)+\sin \left(h\right)\cos \left(x\right)-\sin \left(x\right)}}{{\displaystyle h}}= \\ =\cos \left(x\right)\left[\underset{h\to 0}{\lim }\frac{{\displaystyle \sin \left(h\right)}}{{\displaystyle h}}\right] \end{gathered}$$

Gränsvärdet du försöker lösa med l'Hospitals regel dyker upp i härledningen av derivatan. För referens kan läsas mer här:

Undervisnings-FAQ

Däremot kan l'Hospital vara ett bra sätt att kolla att man fått rätt svar, när man väl har ett svar.

Jag tycker dock det är värt att nämna att l'Hôpitals regel inte alltid ger upphov till cirkelresonemang.

Exempelvis kan gränsvärdet:

$\lim_{x\to0^+}\dfrac{x}{\ln(x)}$

utan problem beräknas med hjälp av l'Hôpitals regel då gränsvärdet inte är nödvändigt för att bevisa derivatan av varken $\ln(x)$ eller $x$.

AlvinB skrev:

Exempelvis kan gränsvärdet:

$\lim_{x\to0^+}\dfrac{x}{\ln(x)}$

utan problem beräknas med hjälp av l'Hôpitals regel ...

Fast där går ju täljaren mot 0 och nämnaren mot -∞, så l'Hospital behövs inte. Jag undrar ens om den kan användas. (Att svaret blir rätt är en annan femma.)

Dr. G skrev:

AlvinB skrev:

Exempelvis kan gränsvärdet:

$\lim_{x\to0^+}\dfrac{x}{\ln(x)}$

utan problem beräknas med hjälp av l'Hôpitals regel ...

Fast där går ju täljaren mot 0 och nämnaren mot -∞, så l'Hospital behövs inte. Jag undrar ens om den kan användas. (Att svaret blir rätt är en annan femma.)

l'Hôpitals regel verkar finnas i femtioelva olika varianter, men enligt formuleringen på Wikipedia räcker det med att endast nämnaren går mot $\infty$ eller $-\infty$ för att få tillämpa l'Hôpitals regel.

Du har dock rätt i att exemplet kanske inte demonstrerar min poäng särskilt väl eftersom det är ganska uppenbart att gränsvärdet är $0$. Kanske skulle jag istället valt gränsvärdet:

$\lim_{x\to1}\dfrac{x-1}{\ln(x)}$