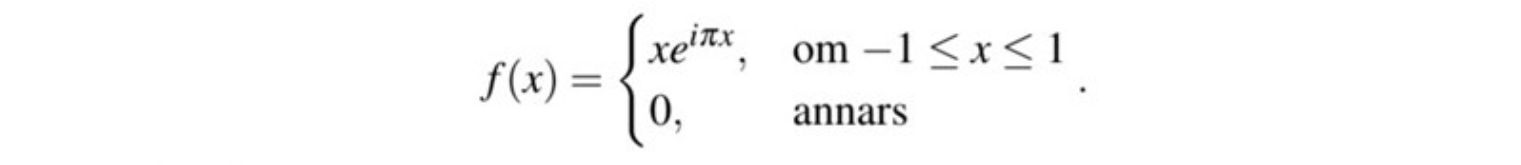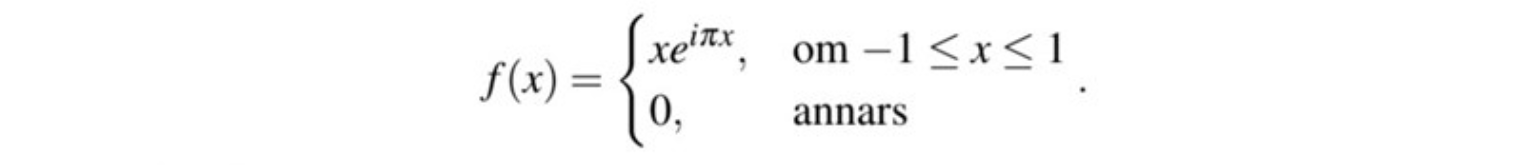Gränsvärdet då x=1/2 och x=1?

Integralen som du ska beräkna påminner om inversionsformeln ("Fundamental theorem of the Fourier Integral" i Beerends bok, eller Theorem 3.3 "Inverse Fourier Transform" i Pinkus–Zafranys bok), eller hur?

Vad säger inversionsformeln?

LuMa07 skrev:

Integralen som du ska beräkna påminner om inversionsformeln ("Fundamental theorem of the Fourier Integral" i Beerends bok, eller Theorem 3.3 "Inverse Fourier Transform" i Pinkus–Zafranys bok), eller hur?

Vad säger inversionsformeln?

På vilket sätt påminner det dig om inversformeln? Såhär står det om definitionen av inverstransformen:

Var god titta på Theorem 3.3

Tänk på att $\mathcal{F}[f](\omega)$ är det som betecknas med $F(\omega)$ i uppgiften.

LuMa07 skrev:

Var god titta på Theorem 3.3

Tänk på att $\mathcal{F}[f](\omega)$ är det som betecknas med $F(\omega)$ i uppgiften.

Vilken är Theorem 3.3? Ja jag vet att F[f](w)=F(w)

Du har lagt upp en skärmdump med sid 108 från Pinkus-Zafranys bok. Gå till sid 109 istället!

LuMa07 skrev:

Du har lagt upp en skärmdump med sid 108 från Pinkus-Zafranys bok. Gå till sid 109 istället!

Ja jag ser nu Theorem 3.3. Hur ska man använda sig av den där theorem?

Använd definitionen av f för att beräkna $\frac{f\left({\displaystyle \frac{1}{2}}+\right)+f\left({\displaystyle \frac{1}{2}}-\right)}{2}$.

PATENTERAMERA skrev:

Använd definitionen av f för att beräkna $\frac{f\left({\displaystyle \frac{1}{2}}+\right)+f\left({\displaystyle \frac{1}{2}}-\right)}{2}$.

Hur använder jag detta?  Vad betyder 1/2+ och 1/2-?

Kolla upp hur boken definierar f(x+) och f(x-). Misstänker att det är höger- och vänstergränsvärde eller liknande. Tillämpa definitionerna på f i problemet.

PATENTERAMERA skrev:

Kolla upp hur boken definierar f(x+) och f(x-). Misstänker att det är höger- och vänstergränsvärde eller liknande. Tillämpa definitionerna på f i problemet.

Ja precis det är höger och vänstergränsvärde de menar här. Men hur ska man tillämpa på f menar du?

Du får tex beräkna $f\left(\frac{1}{2}+\right)=\underset{x\to \frac{1}{2}+}{\lim }f\left(x\right)$. Repetera höger- och vänstergränsvärden om du inte har det aktuellt.

Sedan får du tillämpa det på den funktion f som är given i problemet.

PATENTERAMERA skrev:

Du får tex beräkna $f\left(\frac{1}{2}+\right)=\underset{x\to \frac{1}{2}+}{\lim }f\left(x\right)$. Repetera höger- och vänstergränsvärden om du inte har det aktuellt.

Sedan får du tillämpa det på den funktion f som är given i problemet.

Jag vet hur man beräknar gränsvärde från höger och vänster sida. Men i denna uppgift vet jag inte vilken funktion vi ska använda? 

PATENTERAMERA skrev:

Men här har vi att x=1/2 är mellan -1 och 1. Då x>=1/2 så är det i intervallet 1/2<=x<=1

Ja du kan anta att det är i intervallet 1/2 < x <= 1. Eftersom vi bara är intresserade av vad som händer då vi närmar oss 1/2 mer och mer från positiva sidan.

PATENTERAMERA skrev:

Ja du kan anta att det är i intervallet 1/2 < x <= 1. Eftersom vi bara är intresserade av vad som händer då vi närmar oss 1/2 mer och mer från positiva sidan.

Ja precis båda fall blir det 1/2i och summan av dem blir då( i/2+i/2)/2=i/2

Ja. Sedan har du fallet x = 1. Samma procedur med höger- och vänstergränsvärden.

PATENTERAMERA skrev:

Ja. Sedan har du fallet x = 1. Samma procedur med höger- och vänstergränsvärden.

Ja precis. Gränsvärdet blir dp i/2 respektive 0. Hur ska man svara på det här med egenskaper hos f(x) så att man kan dra slutsats om detta?