Gravitationslagen

 hejsan
hejsan
jag skulle behöva ha lite vägledning i uppgiften.
Det är nog Keplers tredje lag som ska användas i uppgiften.
Jag kan inte riktigt se sammanhanget i det hela.
vart kommer T2/r03 ifrån ? Motsvarar bråket det planetbanornas medelradie R?
Såg nyss att T2jorden = 1 år =365 dagar tar det för jorden att komma tillbaka till samma position i cirkeln
r är planeternas medelradie och T för jorden måste vara 1 år.
 Jag tappade bort mig mot slutet med SI enheterna och 3-roten ur
Jag tappade bort mig mot slutet med SI enheterna och 3-roten ur
det ska bli 149,7 Gm
Det verkar stämma. När du drar tredjegradsroten ur km³ får du svaret i km.
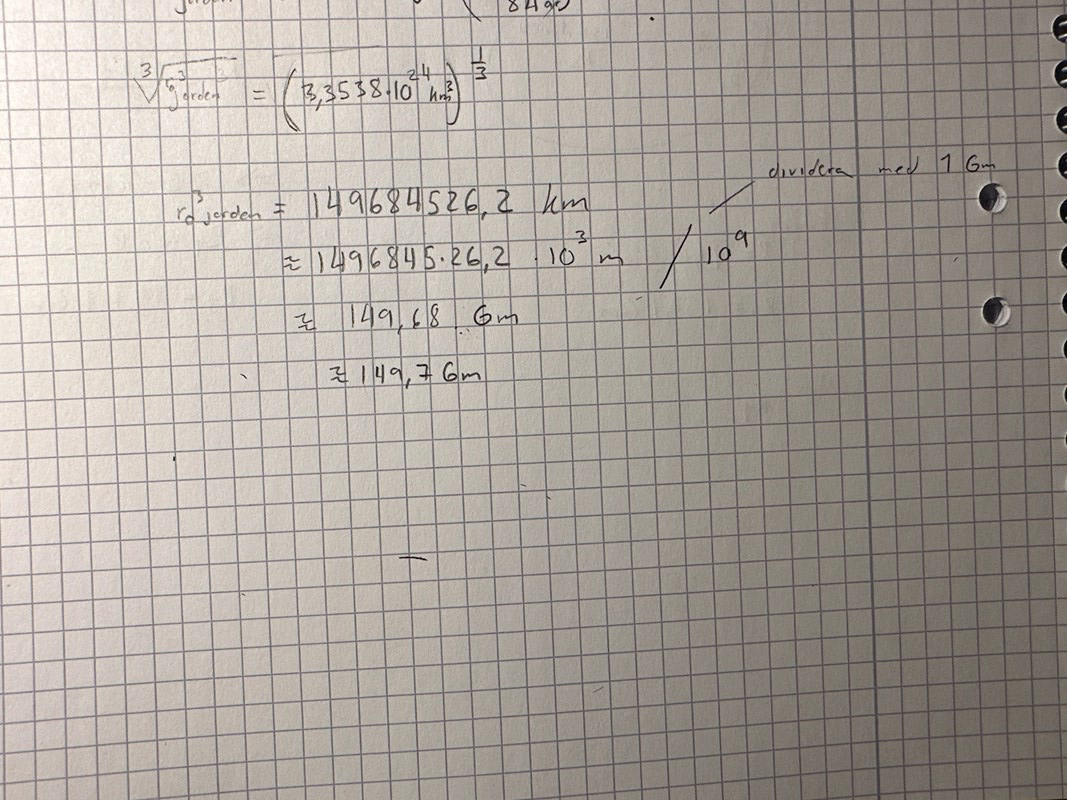 Jag är lite oviss om varför formeln
Jag är lite oviss om varför formeln
T2/r03 (Uranus) = T2/r03 (jorden) tillämpas.
Det ska vara eftersom
Formeln är Keplers tredje lag.
Från den gamla Pluggakuten:
Anta att planeten roterar runt sin stjärna i en cirkulär bana.
Centripetalkraften ges då av uttrycket .
Dragningskraften ges av uttrycket , där stjärnans massa och planetens masssa.
Dessa båda uttryck måste vara lika med varandra, då de beskriver samma kraft.
.
För en cirkulär bana vet vi att
, där är omloppstiden.
Detta innebär att och att och
Eftersom är ett konstant värde, måste även vara konstant.
Keplers tredje lag är därmed härledd.

