Greens
Följande står om Greens sats:
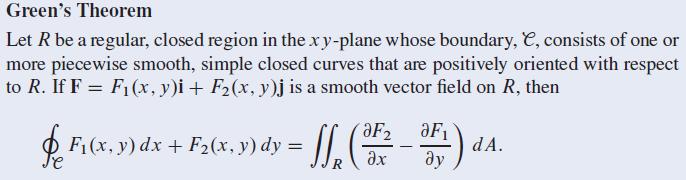
Till uppgiften "Example 2", obs inte "Example 1". Så står det
Jag antar att de använder det tredje vektorfältet från "Example 1". I Greens står det dock att
men hur blir detta lika med ?

Vektorfältet de ansätter är , det vill säga och
Om vi antar att vi har en sluten kurva och vill beräkna kurvintegralen får vi
Var det det du undrade?
D4NIEL skrev:Vektorfältet de ansätter är , det vill säga och
Om vi antar att vi har en sluten kurva och vill beräkna kurvintegralen får vi
Var det det du undrade?
Och detta är ekvivalent med ?
Ja, du kan tänka dig en parameterframställning om det känns lättare.
osv.
D4NIEL skrev:Ja, du kan tänka dig en parameterframställning om det känns lättare.
osv.
Tack återigen Daniel!!

