Greens formel
Behöver hjälp med att förstå "orientering". Jag vet att en Pos.Orient är moturs. och när jag ska använda greens formel så står det i satsen att ϑD ska alltid vara positiv orienterad.
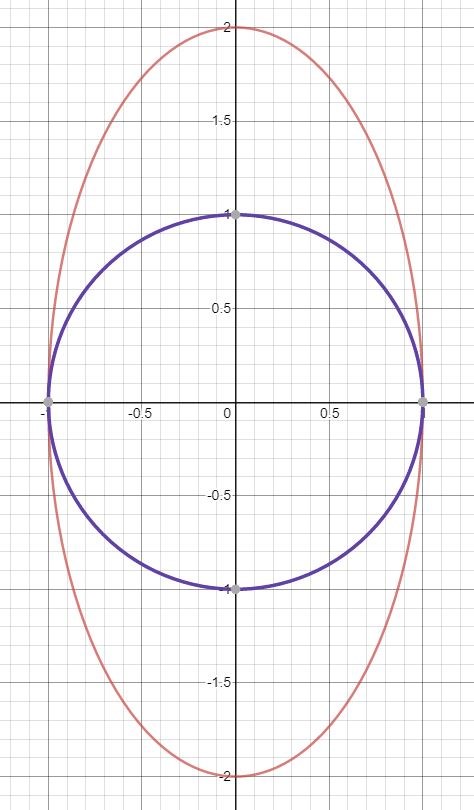
Men, om jag ska t.ex beräkna ett område mellan en ellips och en cirkel så får jag integralen
där är ellipsen och är cirkeln.
Varför är γ2 negativ? ska den inte vara positiv, för att "ϑD alltid ska vara positiv orienterad. "
Att kurvan är positivt orienterad betyder att du hela tiden ska ha det inneslutna integrationsområdet på din vänstra sida när du går runt det.
I vissa fall innebär det att man måste gå mot en av uppgiften definierad riktning eller mot den riktning som ges av växande parametervärden. Allt beror på uppgiftens geometri.
Om du visar den specifika uppgiften kan vi säkert reda ut vad som menas.
Jroth skrev:Att kurvan är positivt orienterad betyder att du hela tiden ska ha det inneslutna integrationsområdet på din vänstra sidan när du går runt det.
I vissa fall innebär det att man måste gå mot den riktning som kurvan i en graf är definierad eller mot den riktning som ges av växande parametervärden. Allt beror på uppgiftens geometri.
Om du visar den specifika uppgiften kan vi säkert reda ut vad som menas.
uppgiften går ut på att man ska beräkna området mellan ellipsen och enhetscirken. Ellipsen löper i positiv led från (1,0) till (0,-2). Alltså den går moturs från (1,0) och går 3/4 av en ellips och slutar vid (0,-2), korrekt?
För att beräkna området så använder jag enhetscirkeln och enligt vad du har förklarat så måste rörelseriktningen för cirkeln vara medurs (för då kommer området ligga till vänster om cirkeln),.alltså kommer integralen vara
där γ1 är ellipsen och γ2 är cirkeln.
har jag gjort rätt eller har jag missforstått något?
BabySoda skrev:
För att beräkna området så använder jag enhetscirkeln och enligt vad du har förklarat så måste rörelseriktningen för cirkeln vara medurs (för då kommer området ligga till vänster om cirkeln),.alltså kommer integralen vara
där γ1 är ellipsen och γ2 är cirkeln. har jag gjort rätt eller har jag missforstått något?
Randkurvan ska utgöras av en eller flera kontinuerligt deriverbara linjestycken som tillsammans ska innesluta (begränsa) ett område, t.ex. det blå området i figuren nedan. Därför måste du sluta randen. Ett exempel på en sådant kurvstycke är med den riktning som anges nedan.
Nu kan du se att det blå området ligger till VÄNSTER om alla linjestycken samt är styckvis glatt (din lärobok kanske pratar om ett kompakt delområde som villkor för Greens formel).
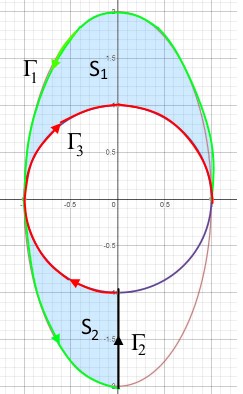
Förutsatt att och är kontinuerligt deriverbara i ett öppet område som håller randen och ytan säger Greens formel nu att
En vanlig parameterframställning av en cirkel är att låta vinkeln växa moturs, vilken betyder att riktningen för i ovanstående bild är motsatt den man normalt sett betraktar som positiv. Alltså måste man justera tecknet om man använder en sådan parameterframställning.
Det är möjligt (och troligt) att linjeintegralen utmed blir , men du måste fortfarande ha med den i ditt resonemang.



