Greens formel

Självklart går det att tröska sig igenom ytintegralerna, men man kan vara lite listig också.

Integraler av typen $\frac{1}{A}{\iint }_{D}x dxdy$ och $\frac{1}{A}{\iint }_{D}y dxdy$ (som eventuellt dyker upp i någon form, *hint*) bör man känna igen som tyngdpunkten av området D i x och y-led.

Arean A av vår triangel är 1. Tyngdpunkten för vår triangel är $x_p=1$ och $y_p=1/3$ (1/3 från basen)

Var noga med att få rätt tecken på det vektoriella ytelementet.

Lycka till!

okej men det är viktigt att lösa uppgiften med hjälp av Greens formel så blir det fortfarande Greens formel om man gör på det sättet?

Annars hade jag tänkt att bestämma AB och BC för att sedan integrera ${\iint }_D\left(y+x\right)dydx$ och där har jag problemet med att få fram gränsvärdena.

Ja, mitt förslag utnyttjar Greens formel (eller Stokes sats). Men istället för att beräkna integralerna inser vi att integralerna beskriver tyngdpunkten för triangeln $(x_p=1, y_p=1/3)$. Låt C vara den slutna kurva som bildas av triangelns sidor genomlupna medurs. Stokes sats ger

${\oint }_{C}F· d\mathbf{r}={\int }_D(\nabla \times \mathbf{F}\mathbf{)}·d\mathbf{S}$

Där D är triangelns område, och $d\mathbf{S}$ är ett ytelement i triangeln med ytnormalens riktning relaterad till omloppsriktningen kring C enligt skruvregeln, dvs

$d\mathbf{S}=-\hat{z}dxdy$

$\nabla \times \mathbf{F}=\hat{z}(x+y)$

Alltså blir vår integral

${\int }_D(\nabla \times \mathbf{F}\mathbf{)}·d\mathbf{S}=-{\iint }_{D}x dxdy-{\iint }_{D}y \mathrm{dxdy}=-x_p-y_p=-\frac{4}{3}$

okej jag är inte helt med på hur vi motiverar val av metod men båda sätten fungerar antar jag. Hur får du fram tyngdpunkten för triangeln till $x_p=1 och y_p=1/3$ ?

Sedan då vi ska beräkna $\nabla \times F=\hat{z}(x+y)$ är $x+y$ det vi får av ${\int }_{D}P\left(x,y\right)dx+Q\left(x,y\right)dy={\iint }_D\left({Q^{´}}_x-{P^{´}}_y\right)dxdy$ och då vi har $P\left(x^2-xy\right) och Q=\left(xy-y^2\right)$ får vi $\left({Q^{´}}_x-{P^{´}}_y\right)=\left(y-\left(-x\right)\right)=y+x$ men var får vi $\hat{z}$ ifrån?

Skulle det gå att lösa uppgiften även med metoden som jag använde tidigare? 

Låt oss ta en lösning i taget. Enligt Greens formel gäller med dina beteckningar:

$\int_{\partial D}P\,dx+Q\,dy=\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right )\,dxdy$

K.Ivanovitj skrev:

${\int }_{D}P\left(x,y\right)dx+Q\left(x,y\right)dy={\iint }_D\left({Q^{´}}_x-{P^{´}}_y\right)dxdy$ och då vi har $P\left(x^2-xy\right) och Q=\left(xy-y^2\right)$ får vi $\left({Q^{´}}_x-{P^{´}}_y\right)=\left(y-\left(-x\right)\right)=y+x$

Ja, du hade fått x+y kvar om randen till området hade varit positivt orienterad. Men om du läser uppgiftstexten noga ser du att det står att vi ska gå runt triangeln medurs. Alltså måste vi byta tecken på integralen eftersom definitionen av Greens formel bygger på en randkurva till ett område som om man följer den i positiv riktning har det begränsade området till vänster om sig. Med dina beteckningar P och Q samt rand och område från figuren nedan får vi:

$-\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right )\,dxdy=-\iint_{D}(x+y)\,dxdy=-\iint_Dx\,dxdy-\iint_Dy\,dxdy$

Är du med på det?

Ett enkelt sätt att komma åt området D är att dela upp det i två delområden, det röda området och det blå området.

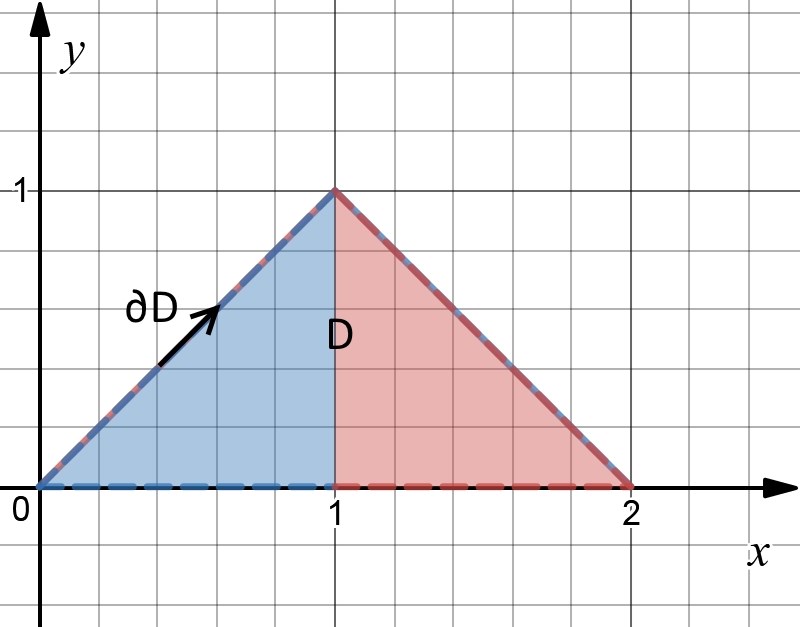
För det blå området gäller att x går från 0 till 1 samtidigt som y ligger mellan 0 och x.

För det röda området gäller att x går från 1 till 2 samtidigt som y ligger mellan 0 och 2-x.

Kan du nu ställa upp integralerna?

okej så ska vi då ställa upp det som $-{\int }_0^1\left(x+y\right)dxdy+{\int }_0^{2-x}\left(x+y\right)dxdy$

Jag förstår inte riktigt hur du tänker. Du verkar sätta ihop områdena på något sätt? Så här tänker jag

För det blå området blir gränserna

$\displaystyle -\int_{x=0}^{1}\int_{y=0}^{x} (x+y)\,dydx$

okej vi får då ${\int }_{x=0}^1$ från triangeln och sedan sätter vi ${\int }_{y=0}^x$   får vi då till det röda området $-{\int }_{x=1}^2{\int }_{y=0}^{2-x}\left(x+y\right)dydx$ 

K.Ivanovitj skrev:

   får vi då till det röda området $-{\int }_{x=1}^2{\int }_{y=0}^{2-x}\left(x+y\right)dydx$ 

 Japp, det är bra, nu återstår alltså att tröska sig igenom de två dubbelintegralerna. Det är inte svårt men lite tidskrävande och tråkigt. Det var därför jag valde en lite annorlunda lösningsgång i mitt ursprungliga lösningsförslag.

okej, jag tror att den första dubbelintegralen ska bli -0.5 dvs $-{\int }_0^1{\int }_0^x\left(x+y\right)dydx=-\frac{1}{2}$  men jag kommer inte fram till det jag fick $-x-\frac{1}{2}$, jag började med att sätta ${\int }_0^{1}ydy+x{\int }_0^{1}1dy={{\overline{)\frac{y^2}{2}}}^1}_0+x{\int }_0^{1}1dy = \frac{1}{2}+x{\int }_0^{1}1dy=\frac{1}{2}+{{\overline{)xy}}^1}_0=x+\frac{1}{2}$ och sedan hade vi ett minustecken framför integralerna så vi får då -x-1/2

Det blev nästan rätt men du har slarvat med gränsen för y. Enligt din ursprungliga integral ska y gå från 0 till x. För den "inre" integralen får du allså (jämför med vad du skriver på rad tre)

$\displaystyle \int_0^x y\,dy+x\int_0^x 1\,dy$

Sedan ska du integrera resultatet av det från x=0 till x=1 (den "yttre" integralen i dubbelintegralen)

ska vi då skriva det som ${{\overline{)\frac{y^2}{2}}}^x}_0+x{\int }_0^{x}1dy$ men jag får det inte att stämma, det känns som att jag blandar ihop lite nu. 

Om man börjar med den första integralen dvs det blå området så ska vi väl ha $-{\int }_0^1{\int }_0^x\left(x+y\right)dydx$

då borde vi väl få $-{\int }_0^{1}ydy+x{\int }_0^{x}1dy$

ska vi sedan ta integralen av y som blir $\frac{y^2}{2}$ så får vi $-{{\overline{)\frac{y^2}{2}}}^1}_0$ = $-\frac{1}{2}$ och sedan har vi kvar $x{\int }_0^{x}1dy$ integralen av 1 blir y och vi får då ${{\overline{)xy}}^x}_0=x^{2}y$

men det blir ju inte rätt svar.

K.Ivanovitj skrev:

ska vi då skriva det som ${{\overline{)\frac{y^2}{2}}}^x}_0+x{\int }_0^{x}1dy$ men jag får det inte att stämma, det känns som att jag blandar ihop lite nu. 

 Ja, det blir lite förvillande med vad man ska sätta in var, men håller man tungan rätt i munnen får man (jag skriver varje term på en rad):

$\displaystyle \int_0^x y\, dy=\left[\frac{y^2}{2}\right]_0^x=(\frac{x^2}{2}-\frac{(0)^2}{2})=\frac{x^2}{2}$

$\displaystyle x\int_0^x 1\,dy=x\left[y\right]_0^x=x\cdot x-x\cdot 0=x^2$

Lägger man ihop det blir det alltså den inre integralen $\int_0^x (x+y)\, dy=\frac{3}{2}x^2$.

Detta ska man sedan integrera från x=0 till 1. (och med minustecken framför såklart). Bidraget från det blå området blir:

$\displaystyle -\int_0^1\int_0^x(x+y)\,dydx=-\int_0^1 \frac{3}{2}x^2\, dx=-\frac{3}{2}\left[\frac{x^3}{3}\right]_0^1=-\frac{3}{6}=-\frac{1}{2}$

Slutligen måste man beräkna bidraget från det röda området också.

okej så vi får alltså att $-{\int }_{x=0}^1{\int }_{y=0}^x\left(x+y\right)dydx= {\int }_0^{x}ydy={{\left[\frac{y^2}{2}\right]}^x}_0=\left(\frac{x^2}{2}\right)=\frac{x^2}{2} och x{\int }_0^{x}1dy=x{{\left[y\right]}^x}_0=x^2$ sätter vi ihop integralerna får vi då $\frac{1}{2}{x}^2+x^2=\frac{3}{2}{x}^2$ sedan integrerar vi från x=0 till 1 och får då $-{\int }_0^1\frac{3}{2}{x}^{2}dx=-\frac{3}{2}{{\left[\frac{x^3}{3}\right]}^1}_0=-\frac{1}{2}$

då har vi alltså gjord det blå området, sedan ska vi även integrera över det röda området

$-{\int }_{x=1}^2{\int }_{y=0}^{2-x}\left(x+y\right)dydx$

ska vi då ställa upp det på samma sätt och få ${\int }_0^{2-x}ydy+x{\int }_0^{2-x}1dy$

Då får jag ${{\left[\frac{y^2}{2}\right]}^{2-x}}_0=\left(\frac{4-x^2}{2}\right)=2-\frac{1}{2}{x}^2$ och sedan $x{\int }_0^{2-x}1dy=x{{\left[y\right]}^{2-x}}_0=x\left(2-x\right)=2x-x^2$ och vi får då den första integralen till $2+2x-\frac{3}{2}{x}^2$

K.Ivanovitj skrev:

Då får jag ${{\left[\frac{y^2}{2}\right]}^{2-x}}_0=\left(\frac{4-x^2}{2}\right)=2-\frac{1}{2}{x}^2$

Här här du slarvat med kvadreringsregeln, tänk på att $(2-x)^2=4-4x+x^2$

Integralen för det blå området blir:

$\displaystyle I=-\int_{x=1}^2\left(\int_{y=0}^{2-x} (x+y)\,dy\right )dx=-\int_{x=0}^1\left[xy+\frac{y^2}{2} \right ]_{y=0}^{2-x}dx=$

$\displaystyle -\int_1^2\left(x(2-x)+\frac{(2-x)^2}{2} \right )dx=-\int_1^2\left(2-\frac{x^2}{2} \right )dx=-\frac{5}{6}$

Slutligen får man den totala ytintegralen för hela triangeln genom att lägga ihop integralen för det blå området med integralen för det röda området.

Som du märkte blev det en del tråkiga räkningar. Kommer man ihåg sin gymnasiegeometri finns det som jag antydde i mitt första inlägg en genomväg. Medianerna i en triangel skär varandra i dess tyngdpunkt. Tyngdpunkten ligger en tredjedel från basen på medianen. För vårt område, D, innebär det $x_p=1,\, y_p=\frac{1}{3}$.

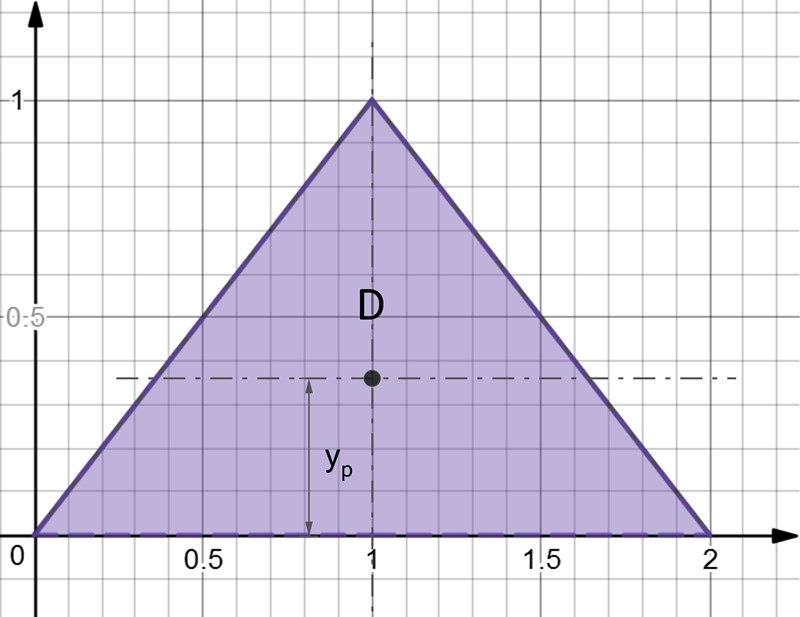
Tyngdpunkten för ett godtyckligt område bestäms av i x- och y-led av $x_p=\frac{1}{A}\iint_D x\,dxdy$ och $y_p=\frac{1}{A}\iint_D y\,dxdy$, där A är områdets totala area. Eftersom arean av triangeln är 1 kan den eftersökta integralen direkt uppfattas som:

$\displaystyle I=-\iint_D(x+y)dxdy=-\iint_Dx\,dxdy-\iint_Dy\,dxdy=-x_p-y_p=-1-\frac{1}{3}=-\frac{4}{3}$

Utan att behöva beräkna en enda integral!

ja det ser onekligen ut som en betydligt bättre väg att lösa uppgiften på.

Jag har lite funderingar bara, hur bestämmer man att D är x=1,y=0.5?är det alltså basen på triangeln som D motsvarar?

och när vi har dubbelintegralerna $-{\iint }_{D}x dxdy - {\iint }_D y dxdy = -x_p-y_p$  varför behöver vi inte sätta några gränsvärden på integralerna när vi använder denna metod? 

minustecknet framför integralerna kommer väl återigen av att vi orienterar medurs?

Dubbelpost

Guggle skrev:

K.Ivanovitj skrev:

ja det ser onekligen ut som en betydligt bättre väg att lösa uppgiften på.

Jag har lite funderingar bara, hur bestämmer man att D är x=1,y=0.5?är det alltså basen på triangeln som D motsvarar?

Triangeln är 2 längdenheter bred och 1 längdenhet hög, se figur. Av symmetri inser vi att tyngdpunkten måste ligga i mitten av basen $x_p=1$ och från gymnasiet kommer vi ihåg att tyngdpunkten för en triangel alltid ligger en tredjedel gånger höjden från basen $y_p=1/3$. Om vi inte vet var tyngdpunkten för en triangel ligger ger inte denna metod någon arbetsbesparing.

 

och när vi har dubbelintegralerna $-{\iint }_{D}x dxdy - {\iint }_D y dxdy = -x_p-y_p$  varför behöver vi inte sätta

 

För att vi  känner igen integralerna som en tyngdpunktsberäkning över området D och vet var tyngdpunkten för en triangel ligger utantill.

 

minustecknet framför integralerna kommer väl återigen av att vi orienterar medurs?

 Ja, det är fortfarande bara Greens formel där randen är orienterad medurs.

  $\displaystyle \int _{\partial D} P\,dx+Q\,dy=-\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right )\,dxdy=-\iint_D(x+y)\,dxdy$