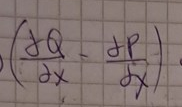Greens formel
Hej!
Jag har lite problem att gå vidare med denna uppgift dels för att jag får derivatan till 0 när jag utför den med greens formel och sen vet jag inte hur jag ska fortsätta då kurvan inte är ett helt varv.
Menar du att den här biten blir noll? Den ska inte vara noll så se till att vara noggrann med tecken när du bestämmer uttrycket.
Minns dock inte helt hur greens sats fungerar och när den används. Tänker annars att det borde gå att lösa med någon parametrisering för ellipsen.
Lasse Vegas skrev:Menar du att den här biten blir noll? Den ska inte vara noll så se till att vara noggrann med tecken när du bestämmer uttrycket.
Minns dock inte helt hur greens sats fungerar och när den används. Tänker annars att det borde gå att lösa med någon parametrisering för ellipsen.
Är du säker på att du har läst kursen? Bara så att jag är säker på att jag får rätt hjälp av en flervarrekunnig PA-användare.
Jag har läst flervarre förut, men det var ett tag sedan dock. Så det är därför jag inte minns allt om till exempel greens sats och stokes sats. Några grejer tittar dock fram såsom att lösa kurvintegraler med parametrisering. Vilket jag tänker borde gå att göra på den här uppgiften :)
Lasse Vegas skrev:Jag har läst flervarre förut, men det var ett tag sedan dock. Så det är därför jag inte minns allt om till exempel greens sats och stokes sats. Några grejer tittar dock fram såsom att lösa kurvintegraler med parametrisering. Vilket jag tänker borde gå att göra på den här uppgiften :)
Men denna uppgift hamnade under greens formel kategori och jag var sugen på att använda den metoden även om kurvintegral vägen finns också.
Då borde det gå att använda greens sats. Vad jag inte minns är att om man ska dra en linje mellan punkterna för att få ett slutet område vilket blir arean man integrerar över. Som sagt, minns inte exakta användning för formeln.
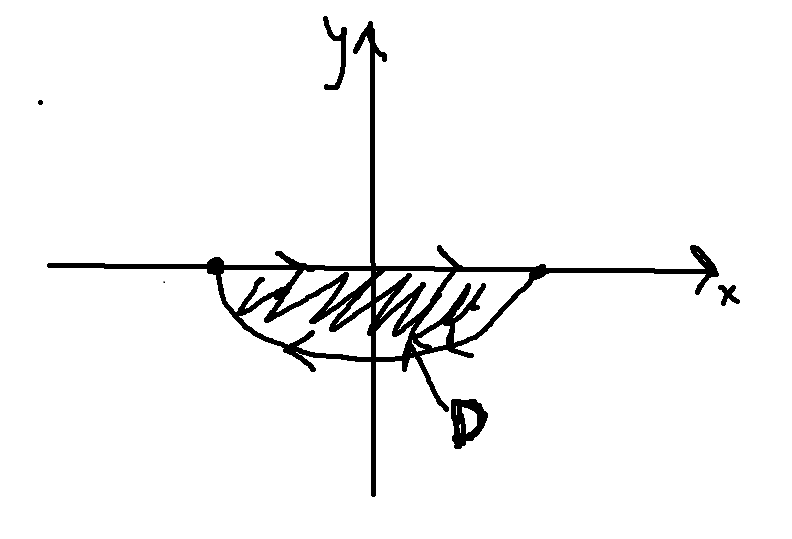
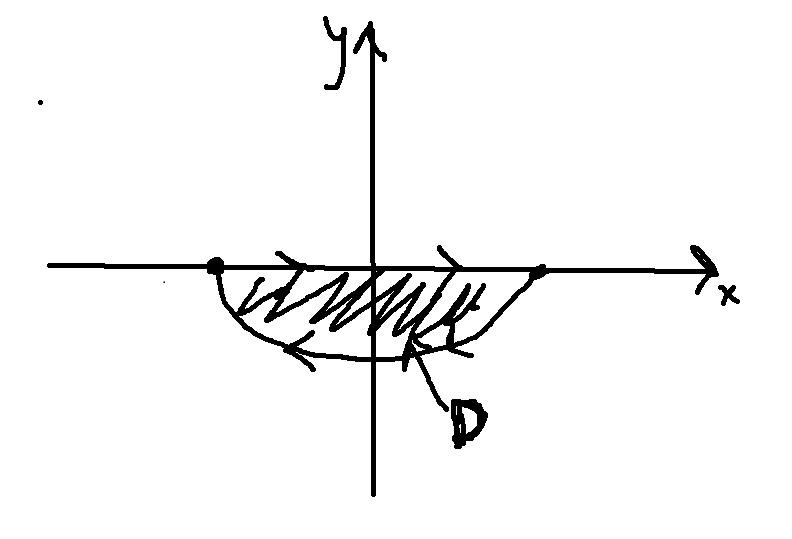
Att området ser ut såhär då.
Edit: som i frågan ska det egentligen vara övre halvan. Pilarna behöver då ändras så att de är orienterade medsols.
Hittade det här dokumentet där de använder greens sats för en öppen kurva: nr18.dvi
Lasse Vegas skrev:
Att området ser ut såhär då.
Edit: som i frågan ska det egentligen vara övre halvan. Pilarna behöver då ändras så att de är orienterade medsols.
Varför såhär och ej övre halvan ?
Råkade rita fel.
Lasse Vegas skrev:Råkade rita fel.
Ah såhär va?
Borde bli så ja.
Här är förresten exempellösningen från dokumentet:
Man utökar alltså kurvan med en linje från ena änden till den andra, men eftersom man lägger till en bit av kurvan behöver man dessutom ta bort samma del.
Lasse Vegas skrev:Här är förresten exempellösningen från dokumentet:
Hur gör jag i mitt fall?
Ställ upp ett uttryck för kurvintegralen över hela kurvan men subtrahera sedan delen du har lagt till. Då kan man använda greens sats på kurvintegralen som löper över hela slutna kurvan.
Så här blir det:
Behöver springa iväg nu. Hoppas det löser sig!
Lasse Vegas skrev:Ställ upp ett uttryck för kurvintegralen över hela kurvan men subtrahera sedan delen du har lagt till. Då kan man använda greens sats på kurvintegralen som löper över hela slutna kurvan.
Såhär typ?
Vad gör jag sen?
Vad använder du parametriseringen till? Vilken del av kurvan används just nu?
Lasse Vegas skrev:Vad använder du parametriseringen till? Vilken del av kurvan används just nu?
(1,0) till (-1,0). Var det inte det vi ska göra eller? Jag vill använda greens formel. Ska man göra så eller hur gör man? Jag är väldigt ny på det här så jag kan ha gjort massa fel eller har missförstått för du redan har glömt detta.
Lasse Vegas skrev:Så här blir det:
Behöver springa iväg nu. Hoppas det löser sig!
Prova att lösa uppgiften på det här sättet. Kurva 1 är den som beskrivs i frågan, kurva 2 är utökningen vi gör för att vi ska få en sluten kurva.
Lasse Vegas skrev:Lasse Vegas skrev:Så här blir det:
Behöver springa iväg nu. Hoppas det löser sig!
Prova att lösa uppgiften på det här sättet. Kurva 1 är den som beskrivs i frågan, kurva 2 är utökningen vi gör för att vi ska få en sluten kurva.
Såhär gjorde jag men jag vet ej om det är rätt eller inte. Jag försökte följa häftet som du skickade innan,dock förstod jag inte hur de bestämde gränserna och kanske har missförstått hur man överhuvudtaget bestämmer gränserna.
Du har gjort framsteg nu. Allt ovanför den svarta linjen stämmer. Men tänk på att området du måste integrera över är det som innesluts av kurvan. Du behöver alltså integrera över en halv ellips vilket går att göra med variabelsubstitution.
Lasse Vegas skrev:Du har gjort framsteg nu. Allt ovanför den svarta linjen stämmer. Men tänk på att området du måste integrera över är det som innesluts av kurvan. Du behöver alltså integrera över en halv ellips vilket går att göra med variabelsubstitution.
Hur ska jag integrera mha en halv ellips?
Grejen med Greens sats är att man gör om en kurvintegral till en dubbelintegral över ett visst område. Sen löser man bara dubbelintegralen som vanligt. Området som du ska integrera över är det som innesluts av kurvan. Området är det som visas i grafen här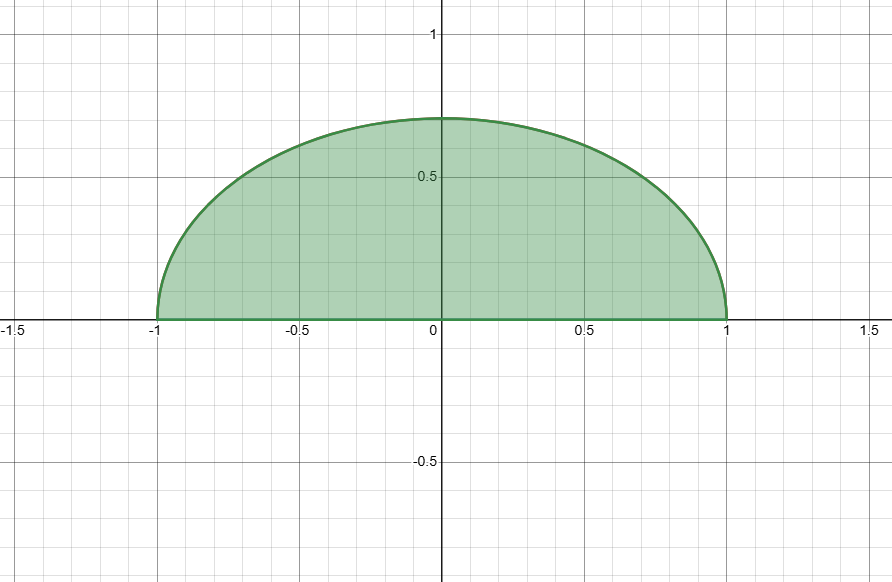
Då behöver man ställa upp lämpliga gränser. Till exempel kan man låta gränsen för y vara
0 =< y =< sqrt[(1-x^2)/2]
och gränsen för x
-1 =< x =< 1.
Men som du kanske minns så brukar det vara lite svårare att integrera över elliptiska och cirkulära områden i xy-koordinatsystemet så man brukar göra ett variabelbyte till någon form av polära koordinater. Då får man istället gränser för radien och vinkeln.
Lasse Vegas skrev:Grejen med Greens sats är att man gör om en kurvintegral till en dubbelintegral över ett visst område. Sen löser man bara dubbelintegralen som vanligt. Området som du ska integrera över är det som innesluts av kurvan. Området är det som visas i grafen här
Yes jag är absolut med på det. Men frågan kvarstår , hur ska jag relatera eller typ använda ellipsen i området? Ska jag gå över till polära koordinater?
Jag var nog otydlig tidigare. När jag sa halva ellipsen så syftade jag på det området som visas i figuren.
Lasse Vegas skrev:Jag var nog otydlig tidigare. När jag sa halva ellipsen så syftade jag på det området som visas i figuren.
Yes men det tickar ingen klocka hos mig fortfarande. Men jag föreslår polära koordinater
x=rcost
y=rsint/2 där t varierar mellan 0 och pi. Och radien varierar mellan -1 och 1? Om det är fel på radie gränserna, hur ska man tänka där?
Är du med på att området i figuren är det som används i Greens sats?
Lasse Vegas skrev:Är du med på att området i figuren är det som används i Greens sats?
Jag tror jag svarade på detta förut. Se #29 och #27
destiny99 skrev:Lasse Vegas skrev:Jag var nog otydlig tidigare. När jag sa halva ellipsen så syftade jag på det området som visas i figuren.
Yes men det tickar ingen klocka hos mig fortfarande. Men jag föreslår polära koordinater
x=rcost
y=rsint/2 där t varierar mellan 0 och pi. Och radien varierar mellan -1 och 1? Om det är fel på radie gränserna, hur ska man tänka där?
Radien kan inte vara negativ, r >= 0 alltid.
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Jag var nog otydlig tidigare. När jag sa halva ellipsen så syftade jag på det området som visas i figuren.
Yes men det tickar ingen klocka hos mig fortfarande. Men jag föreslår polära koordinater
x=rcost
y=rsint/2 där t varierar mellan 0 och pi. Och radien varierar mellan -1 och 1? Om det är fel på radie gränserna, hur ska man tänka där?
Radien kan inte vara negativ, r >= 0 alltid.
Okej
Om du stoppar in din substitution i uttrycket för randen så borde du få [cos(t)]^2 + [sin(t)]^2 = 1. Det säger att randen har radien r = 1. Då vet vi att 0 =< r =< 1.
Lasse Vegas skrev:Om du stoppar in din substitution i uttrycket för randen så borde du få x^2 + y^2 = 1. Det säger att randen har radien r = 1. Då vet vi att 0 =< r =< 1.
Hur menar du nu?
Tog och ändrade, det skulle egentligen stå cos(t) och sin(t). När vi genomför variabelbytet går vi från en ellips i xy-planet till en cirkel i r-t-planet. Den cirkeln vi får har radien 1. Det innebär att vi kan låta r variera mellan 0 och 1 för att täcka cirkeln i r-t-planet och därav täcka ellipsen i xy-planet.
Lasse Vegas skrev:Tog och ändrade, det skulle egentligen stå cos(t) och sin(t). När vi genomför variabelbytet går vi från en ellips i xy-planet till en cirkel i r-t-planet. Den cirkeln vi får har radien 1. Det innebär att vi kan låta r variera mellan 0 och 1 för att täcka ellipsen i xy-planet.
Skulle du kunna visa hur r=0 samt r=1? Vi har ju x^2+2y^2=1
Min parametrisering är såhär
x=rcost
y=rsint/2
Varför valde du just x = rcos(t) och y = rsin(t)/2? Prova att stoppa in det i uttrycket och se vad du får.
Lasse Vegas skrev:Varför valde du just x = rcos(t) och y = rsin(t)/2? Prova att stoppa in det i uttrycket och se vad du får.
Om jag förstod dig rätt så skulle vi göra variabelsubstitution. Du höll alltid med osv så jag vet ej var missförståndet är. Sen sa du att vi ska integrera map på x och y dvs t och r i parametrisering
Jag ifrågasätter inte, det är en ledande fråga. Om du stoppar in substitutionen i uttrycket så kommer det att visa varför r = 1 osv.
Lasse Vegas skrev:Jag ifrågasätter inte, det är en ledande fråga. Om du stoppar in substitutionen i uttrycket så kommer det att visa varför r = 1 osv.
Vilket uttryck ska vi stoppa in?
Parametriseringen du har gjort är till x^2 + 2y^2 = 1. Då kan man stoppa in parametriseringen i uttrycket och se hur det förändras för att dra slutsatser.
Lasse Vegas skrev:Parametriseringen du har gjort är till x^2 + 2y^2 = 1. Då kan man stoppa in parametriseringen i uttrycket och se hur det förändras för att dra slutsatser.
Okej såhär får jag nu. Det stämmer inte med vad du sa eller min parametrisering då
Ja din parametrisering skulle kunna förbättras. Tanken är att man vill få bort nämnaren, så prova att byta ut y mot y = rsin(t)/sqrt(2).
Lasse Vegas skrev:Ja din parametrisering skulle kunna förbättras. Tanken är att man vill få bort nämnaren, så prova att byta ut y mot y = rsin(t)/sqrt(2).
Ok ja. Nu har vi våra gränser från 0 till 1 och sen t går från 0 till pi
Snyggt, sedan integrerar man bara som vanligt.
Jag kom faktiskt precis på ett annat sätt man kan lösa dubbelintegralen på. Om man faktoriserar ut 2:an ur integralen så får man: 
dx dy blir områdets areaelement, om man tar dubbelintegralen av areaelementet över ett område så får man ju områdets area. Dubbelintegralen ger alltså områdets area, vilket skulle kunna bestämmas genom formeln för en ellips area.
Lasse Vegas skrev:Snyggt, sedan integrerar man bara som vanligt.
Som vanligt hur?
Ellipsen area ges produkten av halvaxlarna gånger .
Dessutom visar det sig att linjeintegralen på tillbakavägen (alltså det raka linjestycket utmed x-axeln från (-1,0) till (1,0) är 0 av symmetriskäl).
D4NIEL skrev:Ellipsen area ges produkten av halvaxlarna gånger .
Dessutom visar det sig att linjeintegralen på tillbakavägen (alltså det raka linjestycket utmed x-axeln från (-1,0) till (1,0) är 0 av symmetriskäl).
Jag gick den vägen. Funkar den också? Jag vet inte om det är vad lasse menade med att integrera som vanligt. Fast den integralen blir 0 sen pga sin
