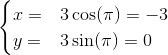Greens formel
Hej
jag har en uppgift som jag har kommit en bit påväg med men skulle behöva lite hjälp.
Låt och beräkna där är den medurs orienterade randen till området
Jag började med att sätta sedan adderade jag i samtliga led och får
Eftersom måste väl y vara positivt och vi får att integrationsområdet är i den första och andra kvadranten.
Jag får då integrationsområdet 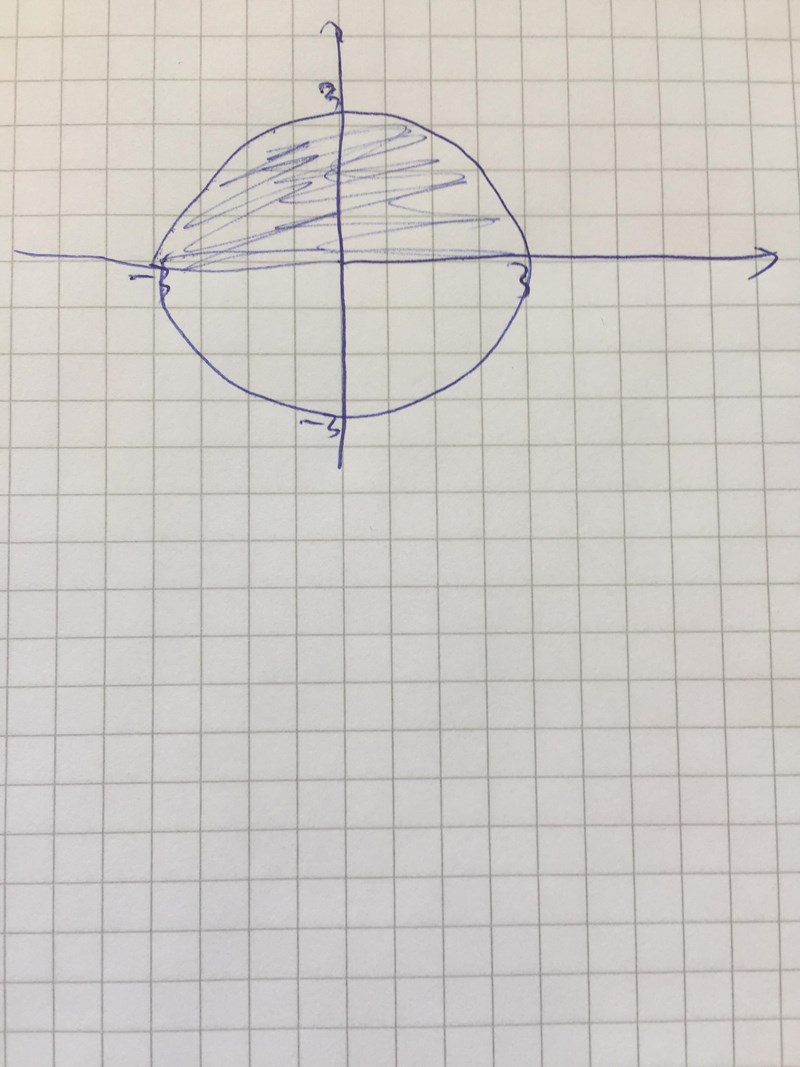
Sedan vill jag gå över till polära koordinater och utnyttja att så att vi får
Sedan har vi att
där =
När man sedan ska tillämpa Greens formel ska man väl sätta vilket i detta fall ger
Därmed ska vi väl integrera dubbelintegralen
ska vi sätta
men jag är inte helt säker på att jag har gjort rätt.
Jag har inte helt kollat igenom vad du arbetat fram, men glöm inte bort att motsatt orientering ger ett minustecken på dubbelintegralen, samt att för att ens få använda Greens formel måste området vara slutet. Just nu är det öppet, du får se till att stänga det (dvs lägg till -3<=x<=3).
jag får då att vi har och med och får vi
men jag är lite osäker på hur man gör när man stänger området, hur ska integralerna bli ? ska vi ha
När du stänger området får du en till KURVINTEGRAL, som går mellan -3 och 3 i x-led och är konstant 0 i y-led.
men får vi inte det om vi har som i exemplet ovan?
eller när ska man använda sig av kurvintegralen? jag är inte riktigt med på hur vi sluter denna integral.
Du kan använda definitionen av kurvintegralen, du vet, vektorfältet skalärt med de komponentvisa derivatorna av parametriseringen av kurvan. Det blir alltså en extra integral du ska beräkna. Det du tänkte beräkna är hela "cirkelskivan" mha Green, men då måste du subtrahera denna nya kurvintegral som du stänger ytan med. Jag är tyvärr inte så bra på att förklara, men hänger du med? Du kan dela upp kurvan.
kan man då först räkna ut hela cirkelskivan först och gå över till polära koordinater så att vi får och integralen och sedan dra ifrån
Nu kan jag ha missat nåt (jag har inte dubbelkollat dina integraler, bara uppställning) men är verkligen kurvintegralen? Har du parametriserat kurvan, deriverat parametriseringen och tagit skalärt med vektorfältet i parametriseringen?
det jag tänkte var om det går att först räkna ut integralen för hela cirkelskivan som jag fick till och sedan dra ifrån
jag är inte helt säker på hur vi får ut rätt kurvintegral så det är möjligt att det inte fungerar som jag tänkt.
Okej, så det du vill göra är följande:
Jag visste inte hur man gjorde "nersänkt" så du får leva med att c, D och phi står lite framför integralerna. Frågan är då, har du koll på hur man beräknar den sista kurvintegralen (över kurvan phi)?
Moffen skrev:Jag visste inte hur man gjorde "nersänkt" så du får leva med att c, D och phi står lite framför integralerna.
Nedanför exponentverktyget finns en symbol som du kan använda för att göra "nedsänkt" :-)

AlvinB skrev:Moffen skrev:Jag visste inte hur man gjorde "nersänkt" så du får leva med att c, D och phi står lite framför integralerna.
Nedanför exponentverktyget finns en symbol som du kan använda för att göra "nedsänkt" :-)
Aha, måste missat den ,tack! :)
okej så om jag läste rätt då med c,D och phi så får vi
där alltså är kurvintegralen vi behöver för att stänga in området genom
gäller det inte att
Jag skrev nåt långt men valde att radera det, det var för förvirrande. Poängen är att din determinant kommer ifrån det blå, och det verkar som att du chansar(?) på definitionen på kurvintegralen. Kurvintegralen är definierad som: , där r(t) är en parametrisering av x och y. Kommer du vidare härifrån? Notera att jag inte heller vet hur man gör pilar över bokstäver, men det ska alltså vara: skalärt, vektorfält och dr med pil ovanför r. Hoppas det är förståeligt annars försöker jag visa mer vad jag menar.
EDIT: Ursäkta hur dåligt det är formaterat. Det skall alltså vara:
men jag trodde att det jag räknade ut i mitt inlägg var parametriseringen, vad är våra värden på r och t annars,? ska man inte sätta r= och t=
Jaha ursäkta, förstod inte vad du menade. Om jag var du skulle jag iallafall parametrisera kurvan phi med t=x, t från -3 till 3 och y=0. Ser du varför/hur?
jag kan inte påstå att jag är helt med men menar du att man ska sätta
Det är ingen dubbelintegral, den sista kurvintegralen (över phi) är en enkel-integral, du ska inte använda greens formel eller nåt sånt, gå rakt utifrån definitionen!
men tar vi bara integralen får vi ju
Är det integralen du får om du i vektorfältet använder parametriseringen, och tar det skalärt med derivatan av parametriseringen? (nej det tror jag inte).
nej jag är inte riktigt med på hur man ska göra här, vårat vektorfält är väl och är det inte parametriseringen vi gör när vi tar
Jag vet tyvärr inte vad du försöker göra nu. Du ska INTE använda Greens sats på kurvintegralen över phi, den beräknar du direkt från definitionen.
Någon får jättegärna rätta mig om jag har fel (läser denna kurs just nu), men jag tror att detta borde vara rätt. Ser du hur jag gjorde? Jämför med definitionen.
Nu råkar F vara 0 utmed hela x-axeln (y=0 där) så för svaret spelar det ingen roll hur många linjeintegraler längs den man drar bort eller lägger till.
Men när man pratar om randen till ett område menar man vanligtvis områdets hela rand om inget annat sägs. I frågan efterfrågas linjeintegralen till randen genomlöpt medurs, dvs linjeintegralen utmed den negativt orienterade randen till området . Området ser ut så här:
Området och dess rand med medurs genomloppsriktning
Randen till området består dels av en halvcirkelbåge, dels av en rät linje från (3,0) till (-3,0).
Området utgör ett kompakt delområde av xy-planet och vektorfältet F är kontinuerligt deriverbar i hela planet. Vi får alltså använda Greens formel (Stokes sats).
så vi kan alltså använda Greens formel utan att dra ifrån något?
blev det rätt när jag räknade ut F*dr=
Det ska vara
okej då får jag
Om vi då har att rot = och vi vill räkna fram så vi har då den första delen.
Den andra delen blir väl då att få fram vilket innebär att vi måste räkna fram
men får att få fram ska vi väl ta derivatan av ytan men jag förstår inte riktigt hur vi ska göra, i andra uppgifter har jag haft en yta z, men nu har vi ju ingen sådan.
Hej!
Uppgiften handlar om att beräkna kurvintegralen
,
där och och är den POSITIVT orienterade randen till området
Om förutsättningarna för Greens teorem är uppfyllda så kan kurvintegralen beräknas som en ytintegral,
K.Ivanovitj skrev:Om vi då har att rot = och vi vill räkna fram så vi har då den första delen.
Den andra delen blir väl då att få fram vilket innebär att vi måste räkna fram
men får att få fram ska vi väl ta derivatan av ytan men jag förstår inte riktigt hur vi ska göra, i andra uppgifter har jag haft en yta z, men nu har vi ju ingen sådan.
Tänk på att rotationen av vektorfältet bara existerar i 3 dimensioner. Om du vill lösa uppgiften med den analoga Stokes sats gäller alltså
Ytan ser vi nu som en tvåsidig glatt yta med randkurva vars omloppsriktning är relaterad till den positiva normalriktningen av ytan. Alltså måste ytnormalen peka i negativ z-led. Ytelementet blir därmed
För vektorfältet , som är kontinuerligt deriverbart i ett öppet område som innehåller och , gäller då enligt Stokes' sats
Albiki skrev:Hej!
Uppgiften handlar om att beräkna kurvintegralen
,
där och och är den POSITIVT orienterade randen till området
Om förutsättningarna för Greens teorem är uppfyllda så kan kurvintegralen beräknas som en ytintegral,
Inför planpolära koordinater för att beräkna ytintegralen.
,
där integrationsområdet är den axelparallella rektangeln
En sak jag funderar över kring , kommer av att rotationen är så vi får men vad blir
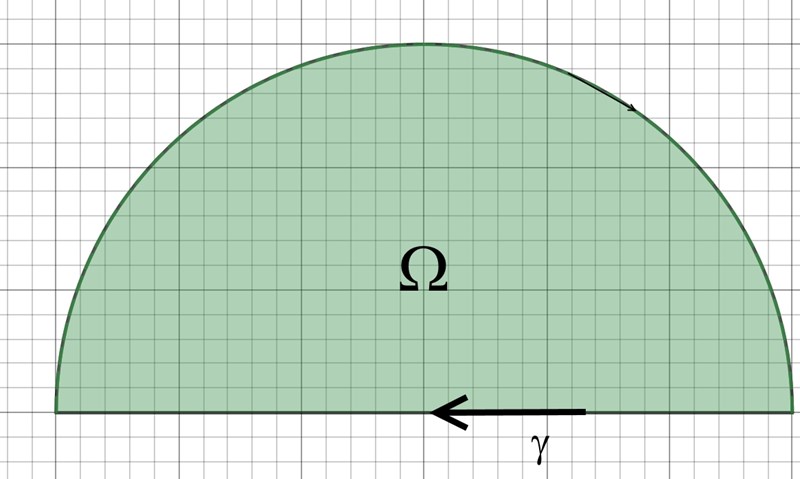
Kan vi då skissa vårat integrationsområde som:
och kan vi då skriva rotationen som
Sedan är jag lite oklar över om vi efter variabelbyte ska använda theta eller phi?
K.Ivanovitj skrev:En sak jag funderar över kring , kommer av att rotationen är så vi får men vad blir
Rotationen av ett vektorfält är en vektor. För att få använda rotation måste du utöka fältet till 3 dimensioner, . Rotationen av just detta vektorfält är
Greens formel är en tvådimensionell fattigmansvariant av Stokes sats. Om du är osäker på Stokes sats och den inte ingår i din kurs bör du använda Greens formel. Om Stokes sats ingår i din kurs måste du lära dig den förr eller senare.
Här är en jämförelse
Om du har ett fält i två dimensioner så är:
Ibland talar man om detta som integralen av differentialformen .
Greens formel säger att om P och Q är kontinuerligt deriverbara i en öppen mängd över en plan yta och C är en rand som omsluter ett delområde D på så sätt att du har området till vänster då du genomlöper C så gäller
I just vårt fall har vi området till höger då vi genomlöper randen. Alltså är integralen du ska beräkna
------------------------------------------------------------------------------------------------------------------------
I tre dimensioner utökar vi vektorfältet . Nu blir rotationen
Notera att du har P och Q från differentialformen på exakt det sätt de förekommer i Greens formel i det tvådimensionella fallet som z-komponent.
Stokes sats säger att om S är en tvåsidig styckvis glatt yta med randkurva C vars genomloppsriktning är sådan att C korrelerar med den positiva normalriktningen av ytan S (dvs om vi går runt C i genomloppsriktningen så ska området ligga till vänster) så gäller
för alla vektorfält som är kontinuerligt deriverbara i ett öppet område som håller S och C.
I det tvådimensionella fallet använder vi ett variabelbyte till planpolära koordinater och funktionaldeterminanten r för att beräkna ytintegralen.
I det tredimensionella fallet låter vi vara en kontinuerlig funktion från ett slutet begränsat område D i till en begränsad sammanhängande punktmängd S i . Punktmängden bildar då en yta i . I vårt fall kan det vara bekvämt att använda som parametrar i parametriseringen.
Området ges naturligtvis av
En enhetsnormal till vår yta är uppenbarligen (vi väljer en normal som orienterar ytan S så att genomloppsriktningen av randen gör att vi har området till vänster om oss).
Det vektoriella ytelementet med rätt normering är därmed
Återigen får vi exakt samma svar.
Sedan är jag lite oklar över om vi efter variabelbyte ska använda theta eller phi?
Du får naturligtvis kalla variablerna i dina variabelbyten vad du vill, men för att det ska bli lättare att förstå är det mer rimligt att kalla radien för eller och vinkeln för eller snarare än tvärtom.
För just denna uppgift ska jag använda Greens formel så då använder jag
när det kommer till våra gränsvärden så får vi ju att våran halvcirkelbåge är i den första och andra kvadranten och går därmed mellan 0 och så vi får men varför får vi att r och inte
och har vi att integrationsområdet D är som bilden
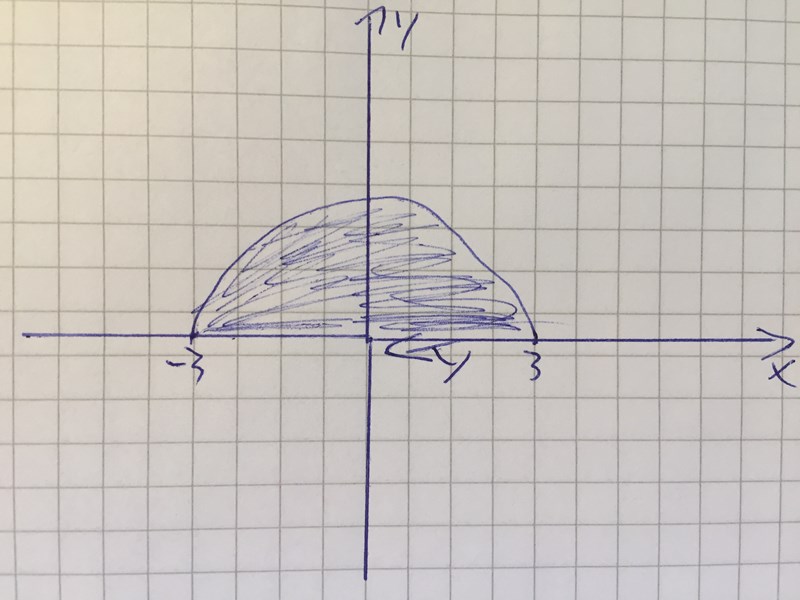
Sedan använder vi väl de två minustecknen till att skriva om till så att vi efter variabelbytet kan sätta och få integralen
K.Ivanovitj skrev: men varför får vi att r och inte
x-koordinaten går från -3 till 3. Men i polära koordinater är r avståndet från origo, det kan aldrig vara mindre än 0.
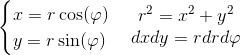
Punkten motsvarar