Greens formel. f(e^x, x^2y)
Tjena, jag stöter på problem med greens formel då denna alltid måste ha ett slutet område och jag förstår inte riktigt när jag ska lägga till respektive ta bort grejer.
Uppgift:
Låt C vara delen av enhetscirkeln från (1, 0) till (0, 1). Beräkna kurvintegralen
Min beräkning:
Figuren är då en kvarts-cirkel i positivt x- & y-led.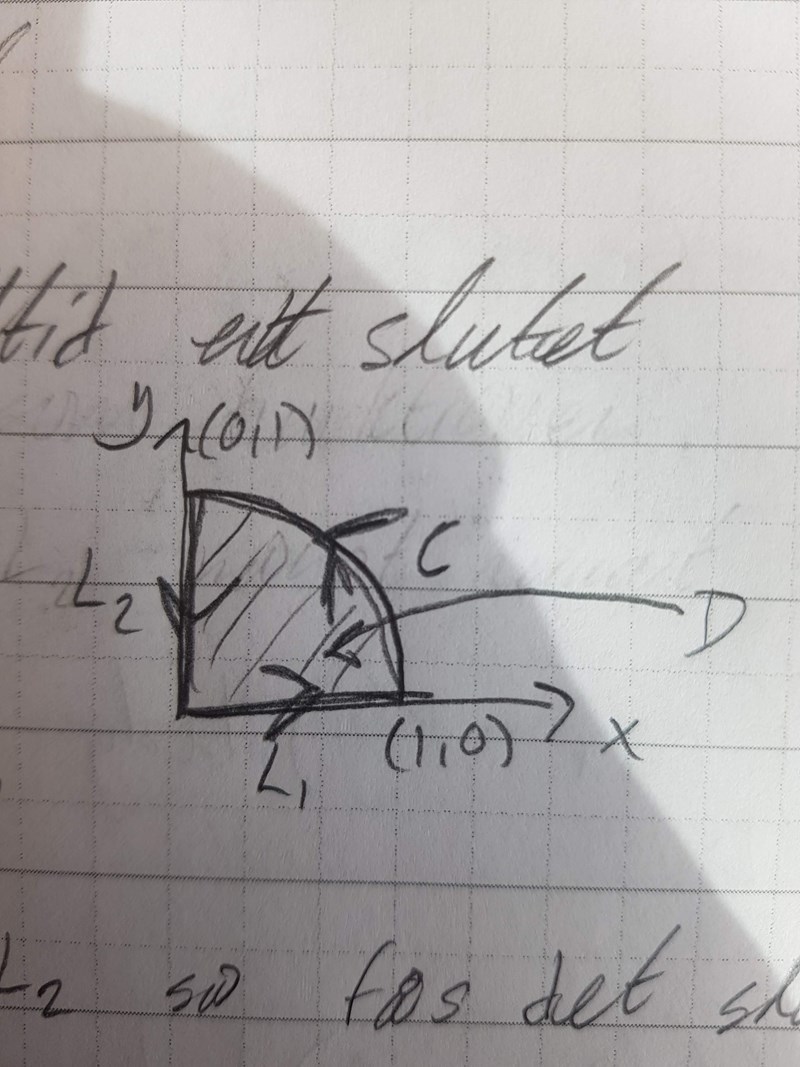
Vad jag har förstått så måste det L1 och L2 läggas till för att få en sluten kurva.
Polära koordinater ger tillslut .
Problem:
trodde jag var för hela kurvan, dvs. C+L1+L2 men den verkar bara vara för C då facit säger att jag måste beräkna integralen för L1 och integralen för L2 dessutom.
Det är något i Greens formel som har med att skapa slutna kurvor som jag tror att jag inte förstår..
Tack på förhand.
Du har nog tänkt rätt. Om du testar räkna ut integralen för raksträckorna kommer du se att de bara råkar bli 0 i just den här uppgiften. Så då är värdet på C lika stort som runt hela.
Micimacko skrev:Du har nog tänkt rätt. Om du testar räkna ut integralen för raksträckorna kommer du se att de bara råkar bli 0 i just den här uppgiften. Så då är värdet på C lika stort som runt hela.
Det är det som inte riktigt blir rätt..
Integralen för L2 = 0 men jag förstår inte riktigt hur medan integralen för L1 blir
Jag förstår inte hur raksträckorna L1 och L2 beräknas. Jag vet att gränserna är för båda sträckorna men funderar på om funktionerna är olika.
Min enda tanke är att L1 har funktionen och att L2 har funktionen , och att jag sedan kör integralerna enligt:
Men integranden för L2 ska bli noll, gör jag något uppenbart fel?
PhilipL skrev:Micimacko skrev:Du har nog tänkt rätt. Om du testar räkna ut integralen för raksträckorna kommer du se att de bara råkar bli 0 i just den här uppgiften. Så då är värdet på C lika stort som runt hela.
Det är det som inte riktigt blir rätt..
Integralen för L2 = 0 men jag förstår inte riktigt hur medan integralen för L1 blirJag förstår inte hur raksträckorna L1 och L2 beräknas. Jag vet att gränserna är för båda sträckorna men funderar på om funktionerna är olika.
Min enda tanke är att L1 har funktionen och att L2 har funktionen , och att jag sedan kör integralerna enligt:
Men integranden för L2 ska bli noll, gör jag något uppenbart fel?
För L2, vad är x där?
Visa spoiler
Du kan parametrisera L2 som y=y och x=0
För L2, vad är x där?
Visa spoiler
Du kan parametrisera L2 som y=y och x=0
Jag ser det absolut men kan man göra parametriseringen tydligare? kanske m.a.p. t?
Du kan kalla y för t om du vill. 0 är 0 oavsett.
Micimacko skrev:Du kan kalla y för t om du vill. 0 är 0 oavsett.
haha jaa, absolut.
Det gäller helt enkelt bara att se att x=0
Hej PhilipL,
Tillsammans med linjerna och innesluter kurvan ett område , vars rand utgörs av de tre kurvorna; du kan skriva detta såhär
.
Du kan tillämpa Greens formel på detta område.
Men kurvintegralen kan skrivas som en summa av tre kurvintegraler
så att Greens formel ger dig den sökta kurvintegralen som
Linjen parameteriseras som
och linjen parameteriseras som
.
Det gör att kurvintegralen längs blir
och att kurvintegralen längs blir
;
notera att startar med och slutar med , medan startar med och slutar med .
Tack! Bra beskrivning!
Ytintegralen blir
Byte till planpolära koordinater ger att området kan skrivas som
och differentialytelementet blir vilket ger ytintegralen som en produkt av två enkelintegraler.
Resultat: Den sökta kurvintegralen blir


