Greens? med en paramatisering
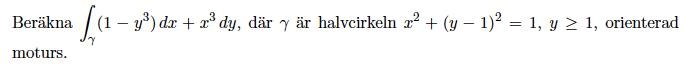

Men jag fastnar vid blir det om $$x^3$ så vi får $$t^3 \cos^3(t)$$ ?</p> <p>och för $$1-y^3 = -1 + t^3 \sin^3(t)$$ ?
En massa dollartecken i det du skrev under bilden så svårt att se vad som står där...
Har du provat att undersöka dP/dx - dQ/dy ? Om det är lika med noll vet vi att kurvintegralen är oberoende av integrationsväg, då är det oftast lättare att parametriera. Är det inte lika med noll brukar det fungera fint med Green
Tomte123 skrev:En massa dollartecken i det du skrev under bilden så svårt att se vad som står där...
Har du provat att undersöka dP/dx - dQ/dy ? Om det är lika med noll vet vi att kurvintegralen är oberoende av integrationsväg, då är det oftast lättare att parametriera. Är det inte lika med noll brukar det fungera fint med Green
Ahh nej. Den är inte lika med noll.
När du använder Greens formel går integralen från att vara en kurvintegral till att vara en dubbelintegral. Du skall alltså beräkna dubbelintegralen
där är området som innesluts av kurvan som du använder Greens formel på. För att beräkna denna dubbelintegral behövs inte någon parametrisering (parametriseringar i en variabel används för att beräkna kurvintegraler).
Observera dock att du enbart får använda Greens formel på slutna kurvor. Är din kurva sluten? Om inte, vad skall du lägga till för att den skall bli det?
AlvinB skrev:När du använder Greens formel går integralen från att vara en kurvintegral till att vara en dubbelintegral. Du skall alltså beräkna dubbelintegralen
där är området som innesluts av kurvan som du använder Greens formel på. För att beräkna denna dubbelintegral behövs inte någon parametrisering (parametriseringar i en variabel används för att beräkna kurvintegraler).
Observera dock att du enbart får använda Greens formel på slutna kurvor. Är din kurva sluten? Om inte, vad skall du lägga till för att den skall bli det?
Det är väl en cirkel? Så därmed sluten?
Är det en hel cirkel?
Hej!
- Du verkar ha helt bortsett från kravet att
- Ekvationen beskriver en cirkel med centrum i punkten och radie , vilken inte stämmer överens med figuren i din bifogade bild.
En möjlig parameterisering av kurvan är där .
Albiki skrev:Hej!
- Du verkar ha helt bortsett från kravet att
- Ekvationen beskriver en cirkel med centrum i punkten och radie , vilken inte stämmer överens med figuren i din bifogade bild.
En möjlig parameterisering av kurvan är där .
Men ändå om det blir det det inte ? Asså jag tänker i ?
Om y=1+sin t så blir y^3 inte lika med sin^3 t.
Albiki skrev:Om y=1+sin t så blir y^3 inte lika med sin^3 t.
Nej men menar det är ju
så
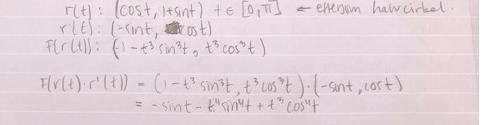
Varför har du potenser av framför och ?
Parametriseringen är ju .
-komponenten i blir då lika med , vilket inte är särskilt lätt att förenkla.
AlvinB skrev:Varför har du potenser av framför och ?
Parametriseringen är ju .
-komponenten i blir då lika med , vilket inte är särskilt lätt att förenkla.
Vänta här nu.. när man paramatiserar r(t) är det du tittar på, eller halvcirkeln ??
mrlill_ludde skrev:AlvinB skrev:Varför har du potenser av framför och ?
Parametriseringen är ju .
-komponenten i blir då lika med , vilket inte är särskilt lätt att förenkla.
Vänta här nu.. när man paramatiserar r(t) är det du tittar på, eller halvcirkeln ??
Det du skriver om F är fel och gör beräkningarna du utfört meningslösa. Objektet F är en vektor (inte ett tal som du skrivit) vars komponenter är 1-y^3 och x^3.
Du har även skrivit att vilket även det är felaktigt.
Om du vill använda parameteriseringen så ska du beräkna skalärprodukten
och integrera denna skalärfunktion över intervallet .
Beräknar du skalärprodukten får du
som kan förenklas till
.
Beräknas integralen får man kurvintegralen till att bli
Albiki skrev:Om du vill använda parameteriseringen så ska du beräkna skalärprodukten
och integrera denna skalärfunktion över intervallet .
men paramatiseringen
kommer den från cirkeln? eller från vektorn???
Parametriseringen utgår från kurvan, d.v.s. cirkeln.


